Wpisany przez Tomasz Lubiński,
12 stycznia 2011 14:13
Każda liczba może zostać jednoznacznie zapisana jako iloczyn liczb pierwszych. Jednoznacznie oznacza, że istnieje tylko jeden zbiór liczb pierwszych, których iloczyn daje w wyniku podaną liczbę. Przy czym możemy tutaj wyróżnić dwa przypadki:
Załóżmy, że mamy daną liczbę x i chcemy rozłożyć ją na czynniki pierwsze. Jak to zrobić?
Potrzebne będą nam dwie dodatkowe zmienne pomocnicze:
Na początku zmienne pomocnicze zainicjujemy następująco:
Teraz tak długo jak i ≤ e będziemy wykonywać następujące kroki:
Po dojściu do granicy pozostaje nam już tylko jedno sprawdzenie: jeżeli x > 1 to wypisz x jako czynnik pierwszy.
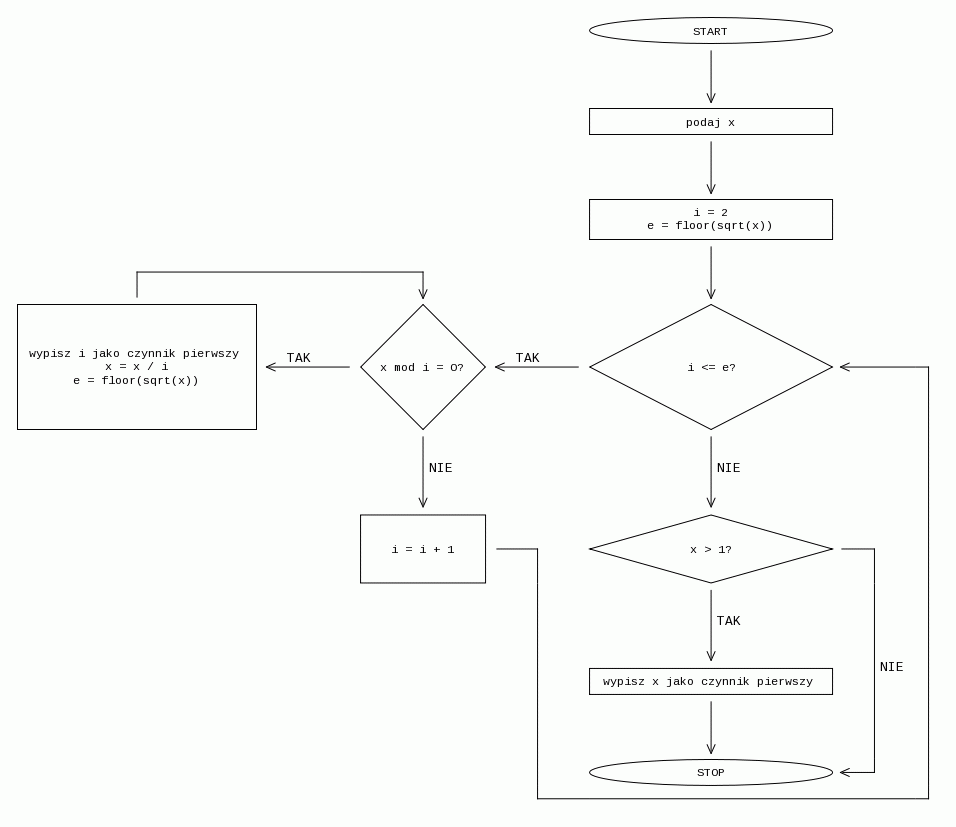
Operację rozkładu liczby x na czynniki pierwsze możemy zapisać następującym schematem blokowym:
Niech x będzie równe 126.
Na początku i = 2, oraz e = floor(sqrt(x)) = floor(sqrt(126)) = floor(11.22497...) = 11.
Dochodzimy do decyzji, czy i ≤ e?
Tak, 2 jest mniejsze lub równe 11, zatem, sprawdzamy kolejną decyzję czy x mod i = 0?:
Tak, 126 mod 2 = 0 (126 jest podzielne przez 2), zatem:
Wypisujemy pierwszy znaleziony czynnik 2, x = x / i = 126 / 2 = 63, e = floor(sqrt(63)) = 7.
Sprawdzamy teraz czy 63 mod 2 = 0?
Nie 63 mod 2 = 1, zatem zwiększamy i o jeden. i = i + 1 = 2 + 1 = 3
Sprawdzamy teraz czy i ≤ e?
Tak, 3 jest mniejsze lub równe 7, zatem, sprawdzamy kolejną decyzję czy x mod i = 0?:
Tak, 63 mod 3 = 0 (63 jest podzielne przez 3), zatem:
Wypisujemy kolejny znaleziony czynnik 3, x = x / i = 63 / 3 = 21, e = floor(sqrt(21)) = 4.
Sprawdzamy teraz czy 21 mod 3 = 0?
Tak, 21 mod 3 = 0 (21 jest podzielne przez 3), zatem:
Wypisujemy kolejny znaleziony czynnik 3, x = x / i = 21 / 3 = 7, e = floor(sqrt(7)) = 2.
Sprawdzamy teraz czy 7 mod 3 = 0?
Nie 7 mod 3 = 1, zatem zwiększamy i o jeden. i = i + 1 = 3 + 1 = 4
Sprawdzamy teraz czy i ≤ e?
Nie 4 nie jest mniejsze lub równe 2.
Zostało nam zatem jeszcze jedno sprawdzenie. Czy x > 1?
Tak 7 jest większe od 1, zatem wypisujemy kolejny znalezion czynnik pierwszy: 7.
Rozłożyliśmy w ten sposób 126 na czynniki pierwsze: 2, 3, 3, 7. Ich iloczyn powinien dać nam 126. 2 * 3 * 3 * 7 = 126.
- liczby złożone - posiadają więcej niż jeden czynnik pierwszy
- liczby pierwsze - posiadają tylko jeden czynnik pierwszy (samą siebie)
Załóżmy, że mamy daną liczbę x i chcemy rozłożyć ją na czynniki pierwsze. Jak to zrobić?
Potrzebne będą nam dwie dodatkowe zmienne pomocnicze:
- i - przez, którą będziemy próbować podzielić daną liczbę, oraz
- e - granicę, do której będziemy zwiększać zmienną i.
Na początku zmienne pomocnicze zainicjujemy następująco:
- i = 2
- e = zaokrąglony w dół pierwiastek kwadratowy z x - jeżeli x jest podzielne przez jakąś liczbę to liczba ta na pewno jest mniejsza od zaokrąglonego w dół pierwiastka kwadratowego z tej liczby.
Teraz tak długo jak i ≤ e będziemy wykonywać następujące kroki:
- tak długo jak x jest podzielne przez i (czyli x mod i = 0), wykonuj następujące kroki:
- wypisz i jako czynnik pierwszy,
- x = x / i, czyli wyrzuć odnaleziony czynnik pierwszy z liczby x
- e = zaokrąglony w dół pierwiastek kwadratowy z x
- zwiększ i o jeden.
Po dojściu do granicy pozostaje nam już tylko jedno sprawdzenie: jeżeli x > 1 to wypisz x jako czynnik pierwszy.
Operację rozkładu liczby x na czynniki pierwsze możemy zapisać następującym schematem blokowym:

Przykład:
Niech x będzie równe 126.
Na początku i = 2, oraz e = floor(sqrt(x)) = floor(sqrt(126)) = floor(11.22497...) = 11.
Dochodzimy do decyzji, czy i ≤ e?
Tak, 2 jest mniejsze lub równe 11, zatem, sprawdzamy kolejną decyzję czy x mod i = 0?:
Tak, 126 mod 2 = 0 (126 jest podzielne przez 2), zatem:
Wypisujemy pierwszy znaleziony czynnik 2, x = x / i = 126 / 2 = 63, e = floor(sqrt(63)) = 7.
Sprawdzamy teraz czy 63 mod 2 = 0?
Nie 63 mod 2 = 1, zatem zwiększamy i o jeden. i = i + 1 = 2 + 1 = 3
Sprawdzamy teraz czy i ≤ e?
Tak, 3 jest mniejsze lub równe 7, zatem, sprawdzamy kolejną decyzję czy x mod i = 0?:
Tak, 63 mod 3 = 0 (63 jest podzielne przez 3), zatem:
Wypisujemy kolejny znaleziony czynnik 3, x = x / i = 63 / 3 = 21, e = floor(sqrt(21)) = 4.
Sprawdzamy teraz czy 21 mod 3 = 0?
Tak, 21 mod 3 = 0 (21 jest podzielne przez 3), zatem:
Wypisujemy kolejny znaleziony czynnik 3, x = x / i = 21 / 3 = 7, e = floor(sqrt(7)) = 2.
Sprawdzamy teraz czy 7 mod 3 = 0?
Nie 7 mod 3 = 1, zatem zwiększamy i o jeden. i = i + 1 = 3 + 1 = 4
Sprawdzamy teraz czy i ≤ e?
Nie 4 nie jest mniejsze lub równe 2.
Zostało nam zatem jeszcze jedno sprawdzenie. Czy x > 1?
Tak 7 jest większe od 1, zatem wypisujemy kolejny znalezion czynnik pierwszy: 7.
Rozłożyliśmy w ten sposób 126 na czynniki pierwsze: 2, 3, 3, 7. Ich iloczyn powinien dać nam 126. 2 * 3 * 3 * 7 = 126.
Przykład w JavaScript:
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C# | MS Visual Studio .net | .cs | .cs | ***** / 5 |
| Tomasz Lubiński | C/C++ | .cpp | .cpp | ***** / 5 | |
| Marian | C/C++ | C++ | .cpp | .cpp | ***** / 5 |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 2 |
| Tomasz Lubiński | Java | .java | .java | ***** / 5 | |
| Tomasz Lubiński | JavaScript | .js | .js | ***** / 3 | |
| Jakub Konieczny | Java_Block | JavaBlock 0.4.6 | .jbf | .jbf | ***** / 2 |
| _marass_ | Php | .php | .php | ***** / 1 | |
| Jakub Konieczny | Python | .py | .py | ***** / 11 |
Poprawiony: 30 stycznia 2013 22:49
Komentarze

+2
#
Borneq
2016-09-28 18:48
Ale dlaczego zwiększamy i o jeden zamiast o dwa? Najpierw badamy podzielność przez 2, potem przez 3, ale potem tylko nieparzyste, to i tak za dużo, bo powinniśmy badać tylko pierwsze.
Odpowiedz | Odpowiedz z cytatem | Cytować
+1
#
Mariusz Jędrzejowski
2019-07-15 15:25
Dlatego wydaje mi się że dla dużego badanego przedziału należy naprzód wygenerować liczby pierwsze wykorzystując sito Atkina. Potem zapisalibyśmy sobie liczby pierwsze do pliku i korzystali z nich w razie potrzeby.
Odpowiedz | Odpowiedz z cytatem | Cytować
Dodaj komentarz


