Wpisany przez Tomasz Lubiński,
14 listopada 2006 00:04
W naiwnym potęgowaniu modulo by obliczyć wartość ab mod n musieliśmy wykonać b mnożeń i dzieleń modulo. Jednak liczbę tą można zredukować do O(log b). Takie obliczanie wartość ab mod n będziemy nazywać szybkim potęgowaniem modulo. Pamiętajmy, że jeżeli a ≥ n to wówczas najpierw obliczymy wartość a mod n a następnie dopiero ją będziemy podnosić do potęgi b.
A więc najpierw rozłóżmy liczbę b na jej postać binarną b = (bm, bm-1, ..., b1, b0)2, gdzie b0 oznacza bit najmłodszy.
Wówczas ab mod n = (ab0 * 20 mod n) * (ab1 * 21 mod n) * ... * (abm-1 * 2m-1 mod n) * (abm * 2m mod n)
Wykorzystamy własność iż: a2m mod n = (a2m-1 * a2m-1) mod n
Zauważmy też, że jeżeli bit x jest równy 0 to wówczas (abx * 2x mod n) = (a0 * 2x mod n) = (a0 mod n) = 1, zatem przemnożyć będziemy musieli tylko te bity, których wartość wynosi 1.
Zatem składając nasze wszystkie spostrzeżenia algorytm szybkiego potęgowania modulo możemy zapisać następująco:
bits = rozloz_na_postac_binarna(b);
m = liczba_bitow(bits);
a = a mod n;
result = 1;
x = a;
for i=0 to m do
begin
if bits[i] = 1 then
begin
result = result * x;
result = result mod n;
end
x = x * x;
x = x mod n;
end;
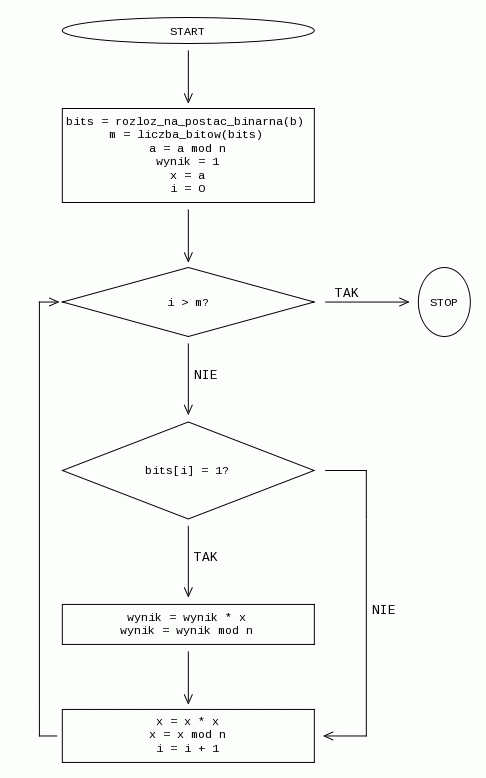
Schemat blokowy przedstawionej metody zapisać można następująco:
Obliczmy 1253 mod 7
53 w zapisie binarnym to (110101)2
Zainicjujmy wszystkie potrzebne zmienne: result = 1, a = 12 mod 7 = 5, x = 5
Teraz obliczenia dla kolejnych bitów:
- b0 = 1, zatem result = 1 * 5 mod 7 = 5, x = 5 * 5 mod 7 = 4
- b1 = 0, zatem x = 4 * 4 mod 7 = 2
- b2 = 1, zatem result = 5 * 2 mod 7 = 3, x = 2 * 2 mod 7 = 4
- b3 = 0, zatem x = 4 * 4 mod 7 = 2
- b4 = 1, zatem result = 3 * 2 mod 7 = 6, x = 2 * 2 mod 7 = 4
- b5 = 1, zatem result = 6 * 4 mod 7 = 3, x = 4 * 4 mod 7 = 2
Czyli ostateczny wynik: 1253 mod 7 = 3
A więc najpierw rozłóżmy liczbę b na jej postać binarną b = (bm, bm-1, ..., b1, b0)2, gdzie b0 oznacza bit najmłodszy.
Wówczas ab mod n = (ab0 * 20 mod n) * (ab1 * 21 mod n) * ... * (abm-1 * 2m-1 mod n) * (abm * 2m mod n)
Wykorzystamy własność iż: a2m mod n = (a2m-1 * a2m-1) mod n
Zauważmy też, że jeżeli bit x jest równy 0 to wówczas (abx * 2x mod n) = (a0 * 2x mod n) = (a0 mod n) = 1, zatem przemnożyć będziemy musieli tylko te bity, których wartość wynosi 1.
Zatem składając nasze wszystkie spostrzeżenia algorytm szybkiego potęgowania modulo możemy zapisać następująco:
bits = rozloz_na_postac_binarna(b);
m = liczba_bitow(bits);
a = a mod n;
result = 1;
x = a;
for i=0 to m do
begin
if bits[i] = 1 then
begin
result = result * x;
result = result mod n;
end
x = x * x;
x = x mod n;
end;
Schemat blokowy przedstawionej metody zapisać można następująco:

Przykład:
Obliczmy 1253 mod 7
53 w zapisie binarnym to (110101)2
Zainicjujmy wszystkie potrzebne zmienne: result = 1, a = 12 mod 7 = 5, x = 5
Teraz obliczenia dla kolejnych bitów:
- b0 = 1, zatem result = 1 * 5 mod 7 = 5, x = 5 * 5 mod 7 = 4
- b1 = 0, zatem x = 4 * 4 mod 7 = 2
- b2 = 1, zatem result = 5 * 2 mod 7 = 3, x = 2 * 2 mod 7 = 4
- b3 = 0, zatem x = 4 * 4 mod 7 = 2
- b4 = 1, zatem result = 3 * 2 mod 7 = 6, x = 2 * 2 mod 7 = 4
- b5 = 1, zatem result = 6 * 4 mod 7 = 3, x = 4 * 4 mod 7 = 2
Czyli ostateczny wynik: 1253 mod 7 = 3
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | Ada | .ada | .ada | ***** / 1 | |
| Tomasz Lubiński | C# | MS Visual Studio .net | .cs | .cs | ***** / 3 |
| Tomasz Lubiński | C/C++ | gotowa funkcja do użycia | .cpp | .cpp | ***** / 16 |
| Kamil Dębowski | C/C++ | dane podawane przez użytkownika | .cpp | .cpp | ***** / 8 |
| Tomasz Lubiński | Delphi/Pascal | .pas | .pas | ***** / 4 | |
| Tomasz Lubiński | Java | .java | .java | ***** / 1 | |
| Adam Chrapkowski | Python | .py | .py | ***** / 5 |
Poprawiony: 26 maja 2010 22:32



gimnazjaliści uczą sie Haskela