Wpisany przez Tomasz Lubiński,
26 kwietnia 2007 21:30
Test pierwszości Fermata to probabilistyczny test umożliwiający sprawdzenie czy dana liczba jest złożona czy prawdopodobnie pierwsza. Jest on jednym z najprostszych testów pierwszości. Oparty jest na małym twierdzeniu Fermata, które mówi, że jeżeli liczba p jest liczbą pierwszą to dla każdego a takiego, że 1≤a<p
a p-1 mod p = 1.
Test Fermata polega na losowym wybraniu liczby a takiej, że 1<a<p i sprawdzeniu czy równość jest prawdziwa (nie ma sensu sprawdzać dla a=1, gdyż dla każdej liczby nierówność będzie prawdziwa). W uproszczeniu możemy to zapisać następująco:
k- określa dokładność testu
p - liczba do sprawdzenia
Algorytm można przedstawić za pomocą następującego schematu blokowego:
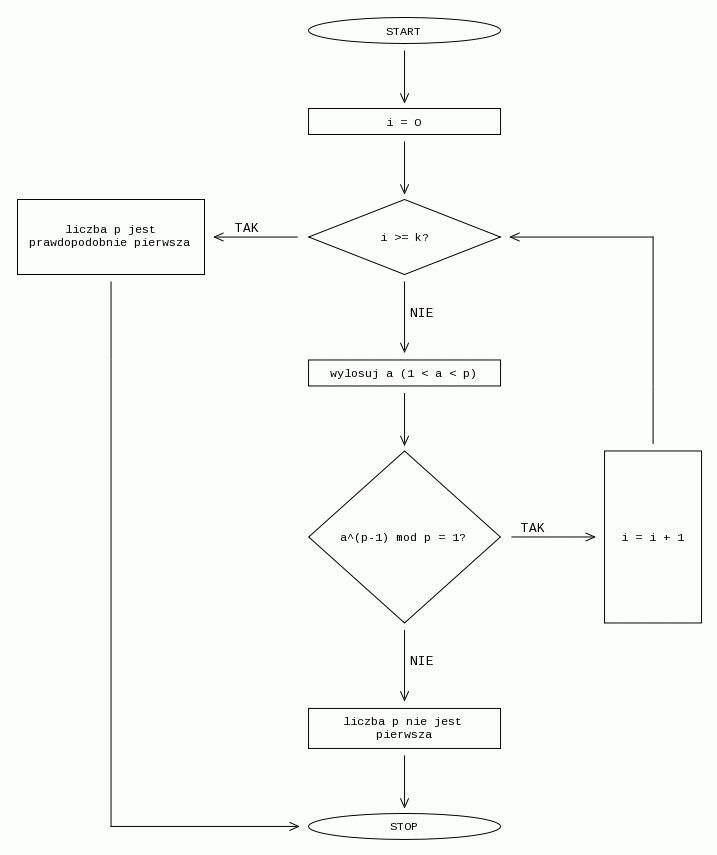
Na pierwszy rzut oka trudność sprawiać może obliczenie wartości ap-1 mod p, szczególnie dla dużych wartości p. Szybko i bezproblemowo obliczymy taką wartość używając algorytmu szybkiego potęgowania modularnego lub dużo wolniejszego, ale prostszego algorytmu naiwnego potęgowania modularnego
Sprawdzimy z dokładnością k=3 czy liczba p=13 jest pierwsza.
Pierwsza próba, wylosowaliśmy a=12. 1212 mod 13 = 1.
Druga próba, wylosowaliśmy a=3. 312 mod 13 = 1.
Trzecia próba, a=4. 412 mod 13 = 1.
Zatem prawdopodobnie liczba 13 jest liczbą pierwszą.
Sprawdzimy z dokładnością k=3 czy liczba p=63 jest pierwsza.
Pierwsza próba, wylosowaliśmy a=8. 862 mod 63 = 1.
W drugiej próbie wylosowaliśmy a=34. 3462 mod 63 = 22.
Równość nie jest spełniona zatem liczba 63, z całą pewnością nie jest liczbą pierwszą.
a p-1 mod p = 1.
Test Fermata polega na losowym wybraniu liczby a takiej, że 1<a<p i sprawdzeniu czy równość jest prawdziwa (nie ma sensu sprawdzać dla a=1, gdyż dla każdej liczby nierówność będzie prawdziwa). W uproszczeniu możemy to zapisać następująco:
k- określa dokładność testu
p - liczba do sprawdzenia
powtórz k razy:
wylosuj a takie, że 1<a<p
sprawdź czy ap-1 mod p = 1
jeżeli nie to przerwij test - liczba nie jest pierwsza
jeżeli równość była spełniona dla wszystkich prób, liczba prawdopodobnie jest pierwsza
Algorytm można przedstawić za pomocą następującego schematu blokowego:

Na pierwszy rzut oka trudność sprawiać może obliczenie wartości ap-1 mod p, szczególnie dla dużych wartości p. Szybko i bezproblemowo obliczymy taką wartość używając algorytmu szybkiego potęgowania modularnego lub dużo wolniejszego, ale prostszego algorytmu naiwnego potęgowania modularnego
Przykład:
Sprawdzimy z dokładnością k=3 czy liczba p=13 jest pierwsza.
Pierwsza próba, wylosowaliśmy a=12. 1212 mod 13 = 1.
Druga próba, wylosowaliśmy a=3. 312 mod 13 = 1.
Trzecia próba, a=4. 412 mod 13 = 1.
Zatem prawdopodobnie liczba 13 jest liczbą pierwszą.
Sprawdzimy z dokładnością k=3 czy liczba p=63 jest pierwsza.
Pierwsza próba, wylosowaliśmy a=8. 862 mod 63 = 1.
W drugiej próbie wylosowaliśmy a=34. 3462 mod 63 = 22.
Równość nie jest spełniona zatem liczba 63, z całą pewnością nie jest liczbą pierwszą.
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | Ada | .ada | .ada | ***** / 1 | |
| Tomasz Lubiński | C# | MS Visual Studio .net | .cs | .cs | ***** / 2 |
| Tomasz Lubiński | C/C++ | .cpp | .cpp | ***** / 6 | |
| Marian | C/C++ | C++ | .cpp | .cpp | ***** / 6 |
| Tomasz Lubiński | Delphi/Pascal | .pas | .pas | ***** / 3 | |
| Tomasz Lubiński | Java | .java | .java | ***** / 3 | |
| _marass_ | Php | .php | .php | ***** / 1 | |
| Adam Chrapkowski | Python | .py | .py | ***** / 1 |
Poprawiony: 26 maja 2010 22:27


