Wpisany przez Michał Knasiecki,
09 sierpnia 2005 21:13
Algorytm Dijkstry służy do wyznaczania najmniejszej odległości od ustalonego wierzchołka s do wszystkich pozostałych w skierowanym
grafie, w odróżnieniu jednak od Algorytmu Forda-Bellmana, graf wejściowy nie może zawierać krawędzi o ujemnych wagach.
W algorytmie tym pamiętany jest zbiór Q wierzchołków, dla których nie obliczono jeszcze najkrótszych ścieżek, oraz wektor D[i] odległości od wierzchołka s do i. Początkowo zbiór Q zawiera wszystkie wierzchołki a wektor D jest pierwszym wierszem macierzy wag krawędzi A.
Algorytm przebiega następująco:
Wprawdzie metoda zachłanna nie zawsze daje wynik optymalny, jednak algorytm Dijkstry jest algorytmem dokładnym.
Oto przyładowy graf oraz jego macierz wag krawędzi (nieskończoność oznacza brak krawędzi):
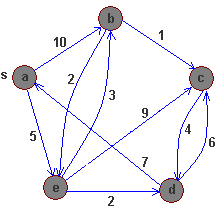

(gwiazdka oznacza symbol nieskończoności, najlżejszy wierzchołek jest podkreślony, wierzchołki, dla których wyznaczono już najkrótsze ścieżki są pogrubione)
Istnieje kilka odmian implementacji Dijkstry; najprostsza używa tablicy do przechowywania wierzchołków ze zbiory Q. Inne wersje algorytmu używają kolejki priorytetowej lub kopca Fibonacciego.
Po znalezieniu najkrótszej odległości między wierzchołkami możemy znaleźć drogę łączącą te wierzchołki za pomocą algorytmu konstrukcji drogi.
Złożoność obliczeniowa: O(n2), przy implementacji bez użycia kopca. Z użyciem kopca można zejść do O(n log n).
W algorytmie tym pamiętany jest zbiór Q wierzchołków, dla których nie obliczono jeszcze najkrótszych ścieżek, oraz wektor D[i] odległości od wierzchołka s do i. Początkowo zbiór Q zawiera wszystkie wierzchołki a wektor D jest pierwszym wierszem macierzy wag krawędzi A.
Algorytm przebiega następująco:
- Dopóki zbiór Q nie jest pusty wykonuj:
- Pobierz ze zbioru Q wierzchołek v o najmniejszej wartości D[v] i usuń go ze zbioru.
- Dla każdego następnika i wierzchołka v dokonaj relaksacji ścieżki, tzn. sprwdź, czy D[i]>D[v]+A[v,i], tzn
czy aktualne oszacowanie odległości do wierzchołka i jest większe od oszacowania odległości do wierzchołka v plus
waga krawędzi (v,i).
Jeżeli tak jest, to zaktualizuj oszacowanie D[i] przypisując mu prawą stronę nierówności (czyli mniejszą wartość).
Wprawdzie metoda zachłanna nie zawsze daje wynik optymalny, jednak algorytm Dijkstry jest algorytmem dokładnym.
Oto przyładowy graf oraz jego macierz wag krawędzi (nieskończoność oznacza brak krawędzi):


(gwiazdka oznacza symbol nieskończoności, najlżejszy wierzchołek jest podkreślony, wierzchołki, dla których wyznaczono już najkrótsze ścieżki są pogrubione)
| Q | D(a) | D(b) | D(c) | D(d) | D(e) |
| {b,c,d,e} | 0 | 10 | * | * | 5 |
| {b,c,d} | 0 | 8 | 14 | 7 | 5 |
| {b,c} | 0 | 8 | 13 | 7 | 5 |
| {c} | 0 | 8 | 9 | 7 | 5 |
| {} | 0 | 8 | 9 | 7 | 5 |
Istnieje kilka odmian implementacji Dijkstry; najprostsza używa tablicy do przechowywania wierzchołków ze zbiory Q. Inne wersje algorytmu używają kolejki priorytetowej lub kopca Fibonacciego.
Po znalezieniu najkrótszej odległości między wierzchołkami możemy znaleźć drogę łączącą te wierzchołki za pomocą algorytmu konstrukcji drogi.
Złożoność obliczeniowa: O(n2), przy implementacji bez użycia kopca. Z użyciem kopca można zejść do O(n log n).
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Michał Knasiecki | C/C++ | .cpp | .cpp | ***** / 29 | |
| Emil Hotkowski | C/C++ | Kopiec Dijkstra , Vectory graf | .cpp | .cpp | ***** / 6 |
| mephisto | Java | .java | .java | ***** / 10 |
Poprawiony: 28 października 2012 15:30



Nie zawsze pierszy, a ten, odleglosci od ktorego szukamy.
ext pisze 'W tabelce przechodząc przez b do c', więc ja się mogę tylko domyślać, co on miał na myśli. Nic w tabelce zamieszczonej na tej stronie nie przechodzi przez nic do niczego - w tabelce są tylko długości najkrótszych tras dla już przebadanej części grafu. Jeżeli on liczy trasy dla a, i przechodzi trasę z b do c, to wychodzi 11.