Wpisany przez Tomasz Lubiński,
09 sierpnia 2005 21:35
Cykl Eulera, to taki cykl w grafie, który zawiera każdą krawędź grafu dokładnie raz. Warunkiem istnienia cyklu są:
Zaczynamy od dowolnego wierzchołka (w naszym przypadku będzie to ten z najmniejszym indeksem), dodajemy ten wierzchołek na stos i idziemy do następnego, osiągalnego z niego wierzchołka z najmniejszym indeksem, a łącząca go z nim drogę usuwamy (rys.1), dodajemy ten wierzchołek na stos i idziemy do następnego, osiągalnego wierzchołka z najmniejszym indeksem, a łączącą go z nim drogę usuwamy (rys.2), itd...
Jeżeli nie możemy już nigdzie pójść pobieramy element ze stosu (będzie on kolejnym w cyklu) i teraz z ostatniego wierzchołka na stosie idziemy dalej (rys. 4). Czynność powtarzamy tak długo jak długo mamy jakieś wierzchołki na stosie.
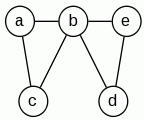
Przebieg algorytmu:
Teraz już nigdzie nie możemy pójść więc zdejmujemy kolejno wierzchołki ze stosu i dodajemy je do cyklu. Końcowy wynik tych operacji to cykl: a,c,b,e,d,b,a.
- spójność grafu,
- dla grafu skierowanego należy sprawdzić czy do każdego wierzchołka wchodzi tyle samo krawędzi co wychodzi
- dla grafu nieskierowanego z każdego wierzchołka musi wychodzić parzysta liczba krawędzi.
Zaczynamy od dowolnego wierzchołka (w naszym przypadku będzie to ten z najmniejszym indeksem), dodajemy ten wierzchołek na stos i idziemy do następnego, osiągalnego z niego wierzchołka z najmniejszym indeksem, a łącząca go z nim drogę usuwamy (rys.1), dodajemy ten wierzchołek na stos i idziemy do następnego, osiągalnego wierzchołka z najmniejszym indeksem, a łączącą go z nim drogę usuwamy (rys.2), itd...
Jeżeli nie możemy już nigdzie pójść pobieramy element ze stosu (będzie on kolejnym w cyklu) i teraz z ostatniego wierzchołka na stosie idziemy dalej (rys. 4). Czynność powtarzamy tak długo jak długo mamy jakieś wierzchołki na stosie.
Przykład:

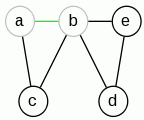
|
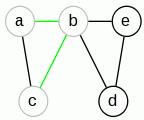
|
Stos: a,b Cykl: |
Stos: a,b,c Cykl: |
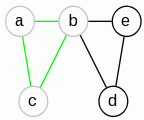
|
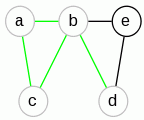
|
Stos: a,b,c,a Cykl: |
Stos: a,b,d Cykl: a,c |

|
|
Stos: a,b,d,e,b Cykl: a,c |
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Emil Hotkowski | C/C++ | C++ - dla grafow nieskierowanych | .cpp | .cpp | ***** / 9 |
| Emil Hotkowski | C/C++ | C++ - na listach krawedzi | .cpp | .cpp | ***** / 3 |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 6 |
Poprawiony: 16 sierpnia 2012 20:22



Graf jest Eulerowski jeżeli wszystkie wierzchołki maja parzysty stopień wierzchołka, i to jest cykl bo przejdziesz wszystkie krawędzie wracając na koniec do początkowej.
(uwaga)
Graf jest półeulerowski jeżeli dwa wierzchołki są nieparzystego stopnia. Jest to tzw. ścieżka eulerowska , czyli droga która zawiera w sobie wszystkie krawędzie jednak zaczyna się i kończy w rożnych wierzchołkach :)
Pozdrawiam :)