Sortowanie topologiczne jest to takie ułożenie na płaszczyźnie wierzchołków grafu, że wszystkie krawędzi biegną od lewa do prawa (lub odwrotnie jak kto chce, ale dla wygody zakładamy że z lewa na prawo).

Poniżej obraz zwykłego grafu.


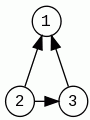
Poniżej obraz grafu po zastosowaniu sortowania topologicznego.



Do sortowania topologicznego zakładamy, iż mamy graf skierowany ACYKLICZNY, tzw. DAG (ang. Directed Acyclic Graph). To iż mamy DAG wiemy że na pewno znajdziemy taki wierzchołek który nie ma żadnych krawędzi wchodzących.
Wyszukujemy taki wierzchołek v, gdzie jego IN[v] = 0. Kładziemy go do "worka", gdzie trzymamy wszystkie takie wierzchołki, następnie wyciągamy pierwszy wierzchołek z tego "worka", wybieramy jego wszystkie krawędzie i usuwamy je z grafu. Jeżeli przez usunięcie jakiś wierzchołek u straci wszystkie krawędzie wchodzące, tzn jego IN[u] = 0 to kładziemy go do "worka".
Krawędzie, które sprawdzamy nigdy nie pokryją się z tymi wierzchołkami które są w "worku". Dlaczego? Proste, te wierzchołki nie mają ŻADNYCH krawędzi wchodzących.

Ale co to jest ten worek? Tym workiem może być cokolwiek: kolejka, lista, nawet kopiec jeżeli chcemy posortować!

Może jakaś alternatywa? Nie podoba mi się taka wersja!
Nie ma problemu. Istnieje sposób wykonania sortowania topologicznego dzięki dfs’owi, czyli przeszukiwaniu grafu w głąb. Wystarczy, że podczas wykonywania jego tradycyjnej wersji będziemy na początek listy dodawać aktualnie przetworzony wierzchołek, a otrzymamy listę w pożądanym porządku.