Wpisany przez Michał Witaszek,
10 czerwca 2012 13:41
Pierwszą rzeczą która kojarzy nam się z potęgowaniem jest dobrze nam znany wzór ogólny działania.
Najprościej opisuje samą operację potęgowania. Na jego podstawie możemy łatwo ułożyć algorytm.
W skrócie algorytm można przedstawić następująco:
Dla a0, zawsze zwróci wartość 1, ponieważ jeszcze przed wykonaniem pętli, do zmiennej wynik przypisaliśmy wartość 1, więc algorytm spełnia założenie:
a0 = 1
Algorytm dokładnie jest opisany na stronach serwisu w artykule potęgowanie.
Jego wadą jest to że nie może zostać użyty do wyliczania potęg z wykładnikami ujemnymi. Możemy jednak łatwo przekształcić powyżej opisaną funkcję korzystając z własności:
Dla przykładu:
2-4 = 1/24 = 1/(2*2*2*2) = 1/16, lub
2-4 = (1/2)4 = 1/2 * 1/2 * 1/2 * 1/2 = 1/16
Lepiej użyć pierwszej własności, ponieważ możemy wykorzystać opisany wcześniej algorytm i na końcu podzielić 1 przez uzyskany wynik, wówczas operację dzielenia wykonamy tylko raz. Ewentualnie moglibyśmy wykonać dzielenie na początku i mnożyć uzyskany ułamek dziesiętny, ale wtedy dopuścilibyśmy większy margines błędu np. 3-n = (1/3)n.
Przekształcając algorytm potęgowania z wykładnikami naturalnymi uzyskujemy funkcję, którą możemy przedstawić następującą listą kroków:
Algorytm różni się tym że zmienna b, czyli wykładnik jest mniejsza od 0, więc będziemy wykonywać pętle dopóki b będzie mniejsze od 0 i przy każdej iteracji, będziemy zwiększać b o 1, zamiast zmniejszać.
Algorytm możemy przedstawić za pomocą następującego schematu:

Powyższa funkcja z kolei może zostać użyta do obliczenia potęg wyłącznie z wykładnikami ujemnymi. Aby wyliczyć potęgi zarówno z wykładnikami dodatnimi jak i ujemnymi, wykorzystamy obydwie funkcje. W ten sposób uzyskujemy algorytm, który można przedstawić za pomocą następującego schematu:
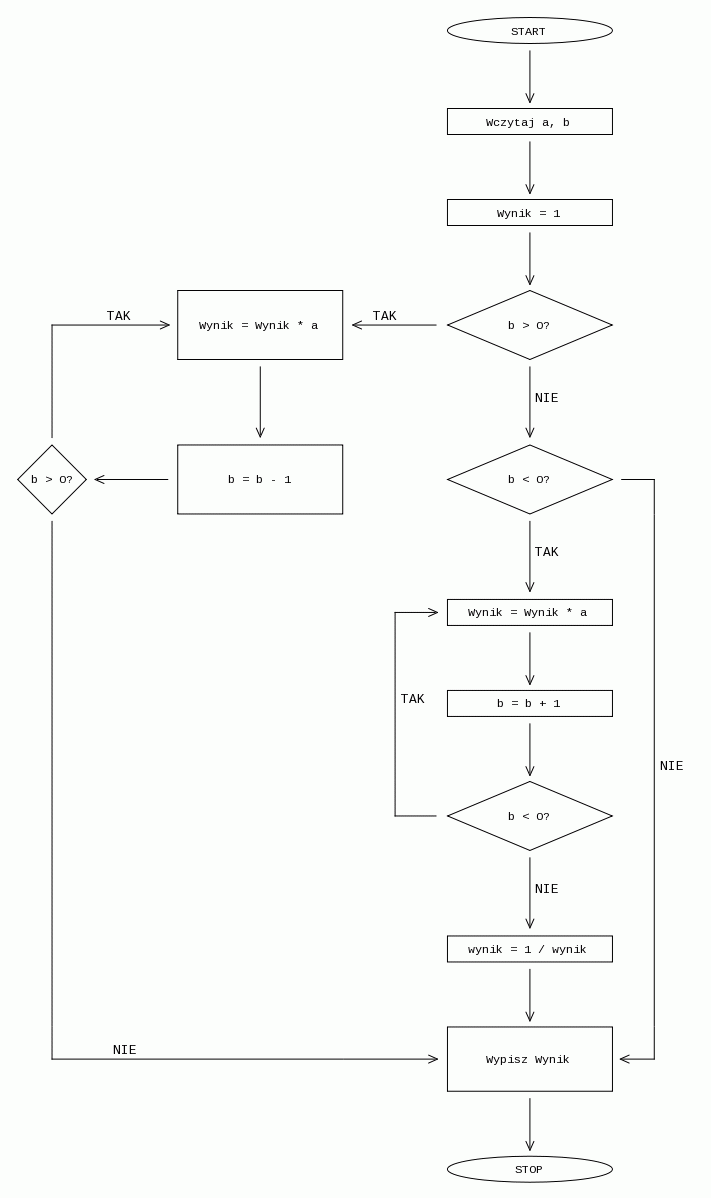
W tym przypadku jeśli wykładnik wynosi 0, algorytm od razu wypisze zmienną wynik by ominąć pętle i nie wykonywać zbędnej iteracji. Podobnie jak wcześniej na początku algorytmu przypisaliśmy do zmiennej wynik wartość 1, więc założenie a0 = 1 zostanie spełnione.
a^{b} = \underbrace{a * a * ... * a}_{ b}
Najprościej opisuje samą operację potęgowania. Na jego podstawie możemy łatwo ułożyć algorytm.
W skrócie algorytm można przedstawić następująco:
- Wczytaj a, b.
- Utwórz zmienną Wynik i nadaj jej wartość 1.
- Dopóki b > 0 do zmiennej Wynik przypisz wartość Wynik * a oraz zmniejsz b o 1.
- Wypisz Wynik.
Dla a0, zawsze zwróci wartość 1, ponieważ jeszcze przed wykonaniem pętli, do zmiennej wynik przypisaliśmy wartość 1, więc algorytm spełnia założenie:
Algorytm dokładnie jest opisany na stronach serwisu w artykule potęgowanie.
Jego wadą jest to że nie może zostać użyty do wyliczania potęg z wykładnikami ujemnymi. Możemy jednak łatwo przekształcić powyżej opisaną funkcję korzystając z własności:
a^{-n}=\frac{1}{a^{n}}=\left(\frac{1}{a}\right)^{n}
Dla przykładu:
2-4 = 1/24 = 1/(2*2*2*2) = 1/16, lub
2-4 = (1/2)4 = 1/2 * 1/2 * 1/2 * 1/2 = 1/16
Lepiej użyć pierwszej własności, ponieważ możemy wykorzystać opisany wcześniej algorytm i na końcu podzielić 1 przez uzyskany wynik, wówczas operację dzielenia wykonamy tylko raz. Ewentualnie moglibyśmy wykonać dzielenie na początku i mnożyć uzyskany ułamek dziesiętny, ale wtedy dopuścilibyśmy większy margines błędu np. 3-n = (1/3)n.
Przekształcając algorytm potęgowania z wykładnikami naturalnymi uzyskujemy funkcję, którą możemy przedstawić następującą listą kroków:
- Wczytaj a, b.
- Utwórz zmienną Wynik i nadaj jej wartość 1.
- Dopóki b < 0 do zmiennej Wynik przypisz wartość Wynik * a oraz zwiększ b o 1.
- Do zmiennej Wynik przypisz wartość 1/Wynik
- Wypisz Wynik.
Algorytm różni się tym że zmienna b, czyli wykładnik jest mniejsza od 0, więc będziemy wykonywać pętle dopóki b będzie mniejsze od 0 i przy każdej iteracji, będziemy zwiększać b o 1, zamiast zmniejszać.
Algorytm możemy przedstawić za pomocą następującego schematu:

Powyższa funkcja z kolei może zostać użyta do obliczenia potęg wyłącznie z wykładnikami ujemnymi. Aby wyliczyć potęgi zarówno z wykładnikami dodatnimi jak i ujemnymi, wykorzystamy obydwie funkcje. W ten sposób uzyskujemy algorytm, który można przedstawić za pomocą następującego schematu:

W tym przypadku jeśli wykładnik wynosi 0, algorytm od razu wypisze zmienną wynik by ominąć pętle i nie wykonywać zbędnej iteracji. Podobnie jak wcześniej na początku algorytmu przypisaliśmy do zmiennej wynik wartość 1, więc założenie a0 = 1 zostanie spełnione.
Przykład w JavaScript:
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Adam Dudzic | C# | .cs | .cs | ***** / 0 | |
| skyfall | C# | .cs | .cs | ***** / 0 | |
| Michał Witaszek | C/C++ | C++ | .cpp | .cpp | ***** / 0 |
| Adam CZ | C/C++ | C++, funkcja obliczająca wynik | .cpp | .cpp | ***** / 2 |
| Michał Witaszek | Delphi/Pascal | .pas | .pas | ***** / 1 | |
| mariuszwroclaw | Java | .java | .java | ***** / 0 | |
| Michał Witaszek | JavaScript | .js | .js | ***** / 0 | |
| seveN. | Php | .php | .php | ***** / 0 | |
| Michał Witaszek | Python | .py | .py | ***** / 1 | |
| Nikodem Solarz | Ruby | metoda obliczająca potęgę (na postawie algorytmu) | .rb | .rb | ***** / 0 |
Poprawiony: 10 czerwca 2012 14:12



Jeśli b = 0 algorytm zwróci wynik z wartością taką jak na początku algorytmu. Na początku ustaliliśmy że wynik=1, więc założenie a^0=1 jest spełnione.
Cytat:
Czytać nie umiesz?!