Wpisany przez Bartosz Bednarczyk,
08 września 2011 14:04
Jednym z pierwszych algorytmów uczonych w szkole jest algorytm potęgowania liczb naturalnych.
Chodzi mianowicie o to, że użytkownik podaje dwie zmienne: a oraz b o wartościach naturalnych, a program ma obliczyć ab. Przychodzi tutaj na myśl własność potęgowania, ze:
Na podstawie tego spostrzeżenia, możemy ułożyć algorytm. Zacznijmy od pseudokodu:
Algorytm ten możemy przedstawić również za pomocą schematu blokowego:
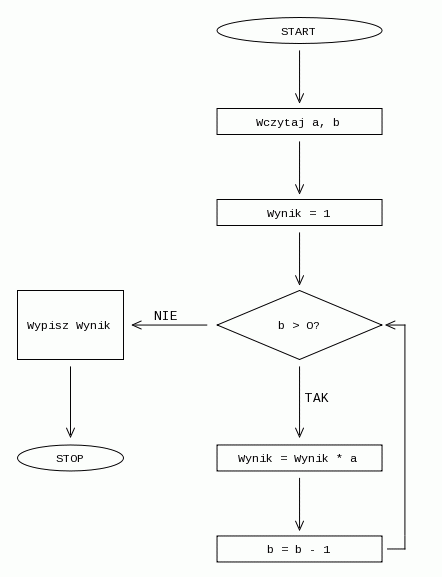
Poniżej zamieszczam tabelę przedstawiającą przebieg algorytmu dla a = 6, b = 3.
Początkowo zmienna a ma wartosc 6, a zmienna b 3. Następnie tworzymy zmienna Wynik, której przypisujemy wartość 1. Następnie wpadamy w pętlę, w której mnożymy wynik i a, a potem zmniejszamy b o 1. Kiedy b będzie równe 0, wychodzimy z pętli i wypisujemy wynik.
Jest to najprostsza wersja potęgowania, wydajniejszy ale też bardziej skomplikowany algorytm opisany jest w artykule: Szybkie potęgowanie modularne
Chodzi mianowicie o to, że użytkownik podaje dwie zmienne: a oraz b o wartościach naturalnych, a program ma obliczyć ab. Przychodzi tutaj na myśl własność potęgowania, ze:
a^{b} = \underbrace{a * a * ... * a}_{ b}
Na podstawie tego spostrzeżenia, możemy ułożyć algorytm. Zacznijmy od pseudokodu:
- Wczytaj a, b.
- Utwórz zmienną Wynik i nadaj jej wartość 1.
- Dopóki b > 0 do zmiennej Wynik przypisz wartość Wynik * a oraz zmniejsz b o 1.
- Wypisz Wynik
Algorytm ten możemy przedstawić również za pomocą schematu blokowego:

Przykład:
Poniżej zamieszczam tabelę przedstawiającą przebieg algorytmu dla a = 6, b = 3.
| a | b | Wynik |
| 6 | 3 | 1 |
| 6 | 2 | 6 |
| 6 | 1 | 36 |
| 6 | 0 | 216 |
Początkowo zmienna a ma wartosc 6, a zmienna b 3. Następnie tworzymy zmienna Wynik, której przypisujemy wartość 1. Następnie wpadamy w pętlę, w której mnożymy wynik i a, a potem zmniejszamy b o 1. Kiedy b będzie równe 0, wychodzimy z pętli i wypisujemy wynik.
Jest to najprostsza wersja potęgowania, wydajniejszy ale też bardziej skomplikowany algorytm opisany jest w artykule: Szybkie potęgowanie modularne
Przykład w JavaScript:
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Bartosz Bednarczyk | C# | .cs | .cs | ***** / 11 | |
| Bartosz Bednarczyk | C/C++ | C | .cpp | .cpp | ***** / 2 |
| Bartosz Bednarczyk | C/C++ | C++ | .cpp | .cpp | ***** / 4 |
| Adam CZ | C/C++ | C++, iteracyjnie | .cpp | .cpp | ***** / 3 |
| Adam CZ | C/C++ | C++, rekurencyjnie | .cpp | .cpp | ***** / 32 |
| Michał Witaszek | Delphi/Pascal | .pas | .pas | ***** / 2 | |
| Bartosz Bednarczyk | Java | .java | .java | ***** / 4 | |
| Dominik Goździuk | Java | wersja rekurencyjna (a^b = a^(b-1)*a) | .java | .java | ***** / 4 |
| Dominik Goździuk | JavaScript | .js | .js | ***** / 15 | |
| Tomasz Lubiński | Java_Block | .jbf | .jbf | ***** / 1 | |
| Dominik Goździuk | Perl | wersja rekurencyjna | .pl | .pl | ***** / 1 |
| Bartosz Bednarczyk | Php | dane z stdin | .php | .php | ***** / 2 |
| seveN. | Php | .php | .php | ***** / 26 | |
| Bartosz Bednarczyk | Python | .py | .py | ***** / 4 | |
| Nikodem Solarz | Ruby | metoda obliczająca wynik potęgowania | .rb | .rb | ***** / 1 |
Poprawiony: 28 października 2012 15:34



Dopóki b mniejsze od 0 do zmiennej Wynik przypisz wartość Wynik * a oraz zwiększ b o 1.