Wpisany przez Tomasz Lubiński,
12 grudnia 2009 15:15
Załóżmy, że mamy dany pewien zbiór odcinków oraz okno, które definiuje nam obszar widziany przez użytkownika. W zależności od wielkości okna oraz jego położenia część odcinków znajdzie się w oknie - powinna zostać pokazana, a część znajdzie się poza oknem - nie powinna być brana pod uwagę. Takie zadanie sprawnie można rozwiązać za pomocą algorytmu Cohena-Sutherlanda.
Końce odcinków zakodujemy zgodnie z rysunkiem poniżej:
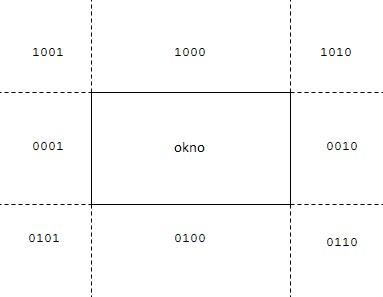
Jeżeli koniec odcinka znajduje się poza oknem:
Jak wynika z rysunku każdy koniec może mieć włączone:
Algorytm Cohena-Sutherlanda działa w następujących krokach.
Na rysunku poniżej przedstawiono proste przypadki wykryte przez algorytm - punkt 2 (odcinki zielone) oraz punkt 3 (odcinki czerwone).

W przypadkach złożonych - punkt 4 postępujemy następująco: wybieramy dowolny koniec o niezerowym kodzie (czyli znajdujący się poza oknem) i na podstawie jego współrzędnych oraz kodu obliczamy punkt przecięcia z osią okna. Jeżeli przyjmiemy, że lewa krawędź okna ma współrzędną x równą LEFT, prawa strona natomiast ma współrzędną x równą RIGHT, oraz analogicznie górna krawędź ma współrzędną y równą TOP, a dolna ma współrzędną y równą BOTTOM, to punkt przecięcia (x, y) dla odcinka o współrzędnych (x1, y1), (x2, y2) obliczymy z następujących wzorów:
W jednym kroku obcinamy odcinek tylko względem jednej krawędzi okna. Po obliczeniu punktu przecięcia odrzucamy część poza oknem, obliczamy nowy kod końca i sprawdzamy, który z przypadków teraz spełnia odcinek. Jeżeli jest to warunek opisany w punkcie drugim, to odrzuciliśmy część będącą poza oknem i została nam już część w całości do pokazania w oknie (odcinki: żółto-niebiesko-żółty, oraz żółto-niebieski na schemacie poniżej), jeżeli jest to warunek opisany w punkcie trzecim to całą resztę również należy odrzucić bo znajduje się poza oknem (odcinek żółty na schemacie poniżej), jeżeli natomiast cały czas odcinek spełnia warunek opisany w punkcie czwartym to musimy dokonać kolejnego cięcia - wykonujemy je tak długo aż nowo powstały odcinek nie spełni warunku z punktu drugiego bądź trzeciego.

Końce odcinków zakodujemy zgodnie z rysunkiem poniżej:

Jeżeli koniec odcinka znajduje się poza oknem:
- z lewej strony - ustaw bit pierwszy,
- z prawej strony - ustaw bit drugi,
- z dołu - ustaw bit trzeci,
- z góry - ustaw bit czwarty.
Jak wynika z rysunku każdy koniec może mieć włączone:
- 0 bitów - znajduje się w oknie,
- 1 bit - znajduje się z boku albo nad albo pod oknem,
- 2 bity - znajduje się z poza oknem pod ukosem.
Algorytm Cohena-Sutherlanda działa w następujących krokach.
- Zakoduj odcinki zgodnie ze wzorem powyżej.
- Jeżeli suma logiczna (or) obydwóch kodów końców odcinka jest równa zero, wówczas cały odcinek mieści się w oknie.
- Jeżeli iloczyn logiczny (and) obydwóch kodów końców odcinka jest różny od zero, wówczas z pewnością cały odcinek mieści się poza oknem.
- W pozostałych przypadkach należy obliczyć punkty przecięcia odcinka z krawędziami okna.
Na rysunku poniżej przedstawiono proste przypadki wykryte przez algorytm - punkt 2 (odcinki zielone) oraz punkt 3 (odcinki czerwone).

W przypadkach złożonych - punkt 4 postępujemy następująco: wybieramy dowolny koniec o niezerowym kodzie (czyli znajdujący się poza oknem) i na podstawie jego współrzędnych oraz kodu obliczamy punkt przecięcia z osią okna. Jeżeli przyjmiemy, że lewa krawędź okna ma współrzędną x równą LEFT, prawa strona natomiast ma współrzędną x równą RIGHT, oraz analogicznie górna krawędź ma współrzędną y równą TOP, a dolna ma współrzędną y równą BOTTOM, to punkt przecięcia (x, y) dla odcinka o współrzędnych (x1, y1), (x2, y2) obliczymy z następujących wzorów:
- jeżeli pierwszy bit jest ustawiony:
y = y_1 + (y_2-y_1) * \frac{LEFT-x_1}{x_2-x_1}\\ x = LEFT
- jeżeli drugi bit jest ustawiony:
y = y_1 + (y_2-y_1) * \frac{RIGHT-x_1}{x_2-x_1}\\ x = RIGHT
- jeżeli trzeci bit jest ustawiony:
x = x_1 + (x_2-x_1) * \frac{BOTTOM-y_1}{y_2-y_1}\\ y = BOTTOM
- jeżeli czwarty bit jest ustawiony:
x = x_1 + (x_2-x_1) * \frac{TOP-y_1}{y_2-y_1}\\ y = TOP
W jednym kroku obcinamy odcinek tylko względem jednej krawędzi okna. Po obliczeniu punktu przecięcia odrzucamy część poza oknem, obliczamy nowy kod końca i sprawdzamy, który z przypadków teraz spełnia odcinek. Jeżeli jest to warunek opisany w punkcie drugim, to odrzuciliśmy część będącą poza oknem i została nam już część w całości do pokazania w oknie (odcinki: żółto-niebiesko-żółty, oraz żółto-niebieski na schemacie poniżej), jeżeli jest to warunek opisany w punkcie trzecim to całą resztę również należy odrzucić bo znajduje się poza oknem (odcinek żółty na schemacie poniżej), jeżeli natomiast cały czas odcinek spełnia warunek opisany w punkcie czwartym to musimy dokonać kolejnego cięcia - wykonujemy je tak długo aż nowo powstały odcinek nie spełni warunku z punktu drugiego bądź trzeciego.

Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C# | MS Visual Studio .net | .cs | .cs | ***** / 2 |
| Andrzej Borucki | C# | MS Visual C# Express 2010 | .cs | .cs | ***** / 0 |
| Tomasz Lubiński | C/C++ | Borland Builder 6 | .cpp | .cpp | ***** / 1 |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 1 |
Poprawiony: 28 sierpnia 2012 20:14


