Wpisany przez Michał Knasiecki,
03 sierpnia 2005 22:34
Czasami zdarza się, że mamy pewien zbiór wierzchołków i musimy go uporządkować względem rosnących kątów nachylenia ich wektorów wodzących do osi OX. Taki porządek jest wykorzystywany np. przy konstrukcji wypukłej otoczki.
Istnieje metoda sortowania takiego zbioru w czasie O(nlogn) porównująca kąty nachylenia bez ich obliczania. Wymaga ona zdefiniowania funkcji alfa:
Niech:
pi (i=1..n) oznacza i-ty punkt w układzie współrzędnych
xi, yi oznaczają współrzędne punktu pi
wprowadźmy także wartość pomocniczą: di=|xi|+| yi|
wówczas funkcję alfa definiujemy:
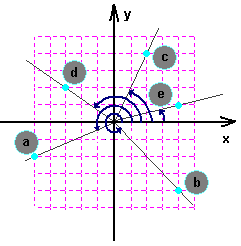
a=(-5, -1), b=(4, -4), c=(2, 4), d=(-3, 2), e=(4, 1)
da=6, db=8, dc=6, dd=5, de=5
Teraz można już wyznaczyć wartość funkcji alfa:
alfaa = 2 + |-1| / 6 = 2.1666
alfab=4 - |-4| / 8 = 3.5
alfac=4 / 6 = 0.6666
alfad=2 - 2 / 5 = 1.6
alfae=1/5=0.2
Po posortowaniu listy punktów wg współczynników alfa otrzymamy szukany ciąg punktów: e, c, d, a, b. Jak widać na rysunku, ciąg ten jest uporządkowany wg kątów wektorów wodzących (część prostej zaznaczonej na szaro ograniczony początkiem układu współrzędnych i punktem). Kąt jest mierzony między wektorem a osią X w kierunku matematycznym, czyli przeciwnym do ruchu wskazówek zegara.
Istnieje metoda sortowania takiego zbioru w czasie O(nlogn) porównująca kąty nachylenia bez ich obliczania. Wymaga ona zdefiniowania funkcji alfa:
Niech:
pi (i=1..n) oznacza i-ty punkt w układzie współrzędnych
xi, yi oznaczają współrzędne punktu pi
wprowadźmy także wartość pomocniczą: di=|xi|+| yi|
wówczas funkcję alfa definiujemy:
alfa_i=
\begin{cases}
\frac{y_i}{d_i} & \text{ gdy } x_i \geq 0 \text{ oraz } y_i \geq 0\\
2-\frac{y_i}{d_i} & \text{ gdy } x_i < 0 \text{ oraz } y_i \geq 0\\
2+\frac{|y_i|}{d_i} & \text{ gdy } x_i < 0 \text{ oraz } y_i < 0\\
4-\frac{|y_i|}{d_i} & \text{ gdy } x_i \geq 0 \text{ oraz } y_i < 0
\end{cases}
Można wykazać, że kąt nachylenia wektora wodzącego punktu pi jest mniejszy od kąta nachylenia wektora wodzącego punktu pj wtedy i tylko wtedy, gdy alfai jest niewiększe od alfaj. Jeśli dwa kilka punktów ma taki sam kąt, wówczas porządkujemy je wg najmniejszych wartości współrzędnej x.Przykład:
a=(-5, -1), b=(4, -4), c=(2, 4), d=(-3, 2), e=(4, 1)

da=6, db=8, dc=6, dd=5, de=5
Teraz można już wyznaczyć wartość funkcji alfa:
alfaa = 2 + |-1| / 6 = 2.1666
alfab=4 - |-4| / 8 = 3.5
alfac=4 / 6 = 0.6666
alfad=2 - 2 / 5 = 1.6
alfae=1/5=0.2
Po posortowaniu listy punktów wg współczynników alfa otrzymamy szukany ciąg punktów: e, c, d, a, b. Jak widać na rysunku, ciąg ten jest uporządkowany wg kątów wektorów wodzących (część prostej zaznaczonej na szaro ograniczony początkiem układu współrzędnych i punktem). Kąt jest mierzony między wektorem a osią X w kierunku matematycznym, czyli przeciwnym do ruchu wskazówek zegara.
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Michał Knasiecki | C/C++ | .cpp | .cpp | ***** / 3 |
Poprawiony: 28 sierpnia 2012 20:03



trzeba pamietac, ze moga sie zdarzyc punkty o tym samym kacie nachylenia i tych samych wspolrzednych x (linia pionowa). Dlatego trzeba dodac porownywanie wspolrzednych y.
czyli dla twojego punktu S:
for po wszystkich punktach P:
{
P.x-=S.x;
P.y-=S.y;
}
W układzie biegunowym drugą współrzędną
jest promień wodzący więc zamiast porządkować punkty względem x
powinniśmy porządkować względem długości
promienia wodzącego