Wpisany przez Michał Knasiecki,
03 sierpnia 2005 22:24
Wypukła otoczka zbioru punktów Q to najmniejszy wypukły wielokąt taki, że każdy punkt ze zbioru Q leży albo na brzegu wielokąta albo w jego wnętrzu.
Oto przykład:
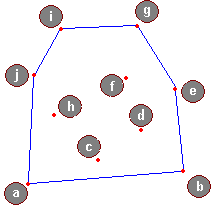
Przeanalizujemy teraz algorytm Grahama, zakładamy przy tym, że zbiór Q jest uporządkowany w następujący sposób:
Na poniższym rysunku widać proste zawierające wektory wodzące punktów, z kątów których wynika przyjęty porządek:
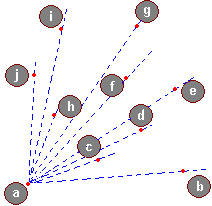
Niech S1 oznacza element na szczycie stosu a S2 element pod nim
m- liczba punktów
pi (i=0...m) oznacza i-ty punkt z uporządkowanej listy (w analogii do rysunku: p0=a, p1=b itd...) K oznacza kąt między punktami S2, S1 oraz pi
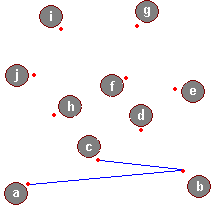
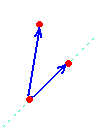 Np. zał. że na szczycie stosu mamy punkt b a tuż pod nim punkt a. Kolejnym punktem do przeanalizowania jest punkt c, chcemy sprawdzić, czy przechodząc do tego punktu (z punktu b) skręcimy w lewo, czy w prawo. Tworzymy więc dwa wektory AB oraz AC (zob. rysunek). Następnie za pomocą wyznaczników sprawdzamy po której stronie wektora AB leży punkt c. W przykładzie z rysunku wyznacznik det(a,b,c)>0 (gdyż punkt c leży po lewej stronie wektora). A zatem przechodząc z punktu b do punktu c skręcimy w lewo.
Np. zał. że na szczycie stosu mamy punkt b a tuż pod nim punkt a. Kolejnym punktem do przeanalizowania jest punkt c, chcemy sprawdzić, czy przechodząc do tego punktu (z punktu b) skręcimy w lewo, czy w prawo. Tworzymy więc dwa wektory AB oraz AC (zob. rysunek). Następnie za pomocą wyznaczników sprawdzamy po której stronie wektora AB leży punkt c. W przykładzie z rysunku wyznacznik det(a,b,c)>0 (gdyż punkt c leży po lewej stronie wektora). A zatem przechodząc z punktu b do punktu c skręcimy w lewo.
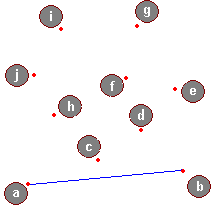
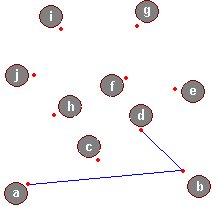
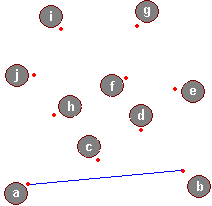
Przeanalizujemy teraz kilka kroków algorytmu, dany jest uporządkowany ciąg punktów:
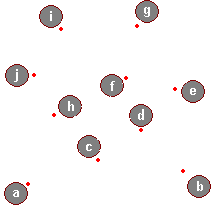
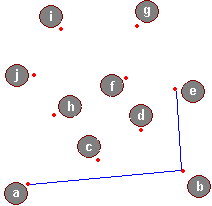
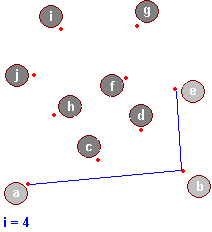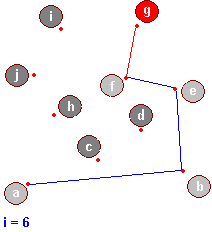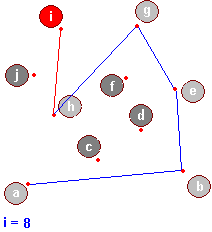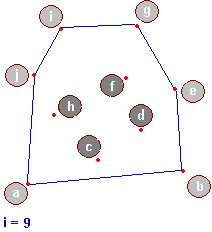
Oto przykład:

Przeanalizujemy teraz algorytm Grahama, zakładamy przy tym, że zbiór Q jest uporządkowany w następujący sposób:
- wierzchołek o najmniejszym indeksie (u nas a) ma najmniejszą wartość y (jeśli jest kilka wierzchołków o najmniejszej wartości y, wybieramy skrajnie lewy)
- kolejne wierzchołki (u nas b do j) są posortowane ze względu na kąt nachylenia ich wektorów wodzących do osi X
Na poniższym rysunku widać proste zawierające wektory wodzące punktów, z kątów których wynika przyjęty porządek:

- jeżeli odchylenie nastąpiło w prawą stronę, zdejmowany jest wierzchołek ze stosu
- jeżeli odchylenie nastąpiło w stronę lewą, wierzchołek pozostaje na stosie
Niech S1 oznacza element na szczycie stosu a S2 element pod nim
m- liczba punktów
pi (i=0...m) oznacza i-ty punkt z uporządkowanej listy (w analogii do rysunku: p0=a, p1=b itd...) K oznacza kąt między punktami S2, S1 oraz pi
- Umieść na stosie punkty p0, p1 i p2
- for i=3 to m do {
- while K oznacza skręt w prawo
- do Usuń punkt ze stosu
- Dodaj na stos punkt pi
- }
 Np. zał. że na szczycie stosu mamy punkt b a tuż pod nim punkt a. Kolejnym punktem do przeanalizowania jest punkt c, chcemy sprawdzić, czy przechodząc do tego punktu (z punktu b) skręcimy w lewo, czy w prawo. Tworzymy więc dwa wektory AB oraz AC (zob. rysunek). Następnie za pomocą wyznaczników sprawdzamy po której stronie wektora AB leży punkt c. W przykładzie z rysunku wyznacznik det(a,b,c)>0 (gdyż punkt c leży po lewej stronie wektora). A zatem przechodząc z punktu b do punktu c skręcimy w lewo.
Np. zał. że na szczycie stosu mamy punkt b a tuż pod nim punkt a. Kolejnym punktem do przeanalizowania jest punkt c, chcemy sprawdzić, czy przechodząc do tego punktu (z punktu b) skręcimy w lewo, czy w prawo. Tworzymy więc dwa wektory AB oraz AC (zob. rysunek). Następnie za pomocą wyznaczników sprawdzamy po której stronie wektora AB leży punkt c. W przykładzie z rysunku wyznacznik det(a,b,c)>0 (gdyż punkt c leży po lewej stronie wektora). A zatem przechodząc z punktu b do punktu c skręcimy w lewo.Przeanalizujemy teraz kilka kroków algorytmu, dany jest uporządkowany ciąg punktów:







Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Michał Knasiecki | C/C++ | .cpp | .cpp | ***** / 9 | |
| Emil Hotkowski | C/C++ | Graham + Sortowanie kątowe | .cpp | .cpp | ***** / 7 |
| Jakub Konieczny | Java_Block | uproszczona metoda | .jbf | .jbf | ***** / 3 |
Poprawiony: 20 czerwca 2011 21:36



A niekiedy nie powinien.
jeżeli odchylenie nastąpiło w stronę lewą, wierzchołek pozostaje na stosie”
To bardzo niejasny fragment, dużo łatwiej by szło zrozumieć gdyby kryterium nie był „skręt w lewo / prawo”, tylko różnica odległości aktualnego i poprzedniego punktu od a (czyli dla a=(0,0) to będzie długość wektora wyznaczającego punkty p_i i p_i-1)
Nic dziwnego skoro p. Knasiecki myli
układ biegunowy z kartezjańskim
Punkty powinny zostać posortowane względem miar kątów nachylenia do osi biegunowej, natomiast punkty współliniowe
względem długości promienia wodzącego