Wpisany przez Michał Knasiecki,
01 sierpnia 2005 23:03
Zał. że dany jest labirynt i dwa różne punkty położone na jego
obwodzie. Jak znaleźć najkrótszą drogę między nimi? Jest to bardzo proste.
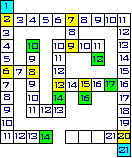
Wczytujemy labirynt do tablicy dwuwymiarowej typu całkowitego. Miejsca wolne (w pliku reprezentowane przez np. spację) zapisujemy jako 0, miejsca zablokowane (reprezentowane np. znakiem "x") jako -1. Następnie na obwodzie tablicy szukamy dwóch punktów o wartości 0 -wejścia i wyjścia (na rysunku kolor niebieski).
Ustawiamy zmienną pomocniczą licznik na 1. Będzie ona symbolizowała aktualną odległość od wejścia.
Przypisujemy tablicy wartość zmiennej licznik w miejscu, gdzie znajduje się wejście (w naszym przypadku [2,1]). Dołączamy współrzędne wejścia do kolejki. Tu zaczyna się pętla: pobieramy z początku kolejki współrzędne pewnego punktu. Sprawdzamy w tablicy, gdzie można iść z tego punktu, tzn. szukamy dookoła punktu, w którym się znajdujemy indeksów o wartości 0. Jeśli znajdziemy taki punkt nad naszą pozycją, to znaczy, że możemy iść w górę, jeżeli na lewo od naszego punktu, to możemy iść w lewo, itd... W ogólności takich punktów może być od 0 do 4. Indeksom, o wartościach 0 (jeśli taki istnieją) przypisujemy wartość zmiennej licznik i zwiększamy licznik o 1. Współrzędne tych punktów (które przed chwilą miały wartość 0) dołączamy na koniec kolejki i przechodzimy na początek pętli (czyli pobieramy z początku kolejki punkt i sprawdzamy, gdzi możemy iść). Robimy to tak długo, aż dojdziemy do wyjścia, tzn. współrzędne naszej aktualnej pozycji i wyjścia są równe.
Na rysunku kolor żólty oznacza rozwidlenia a zielony- miejsca z których nie można już nigdzie iść. Gdy dojdziemy do wyjścia zmienna licznik będzie zawierała najkrótszą odległość od wejścia (u nas 21).
Przeanalizujmy teraz kilka kroków algorytmu dla labiryntu z powyższego rysunku.
Przypisujemy zmiennej licznik wartość 1. Niech Q będzie zbiorem par liczb- współrzędnych punktów. Zbiór Q będzie symbolizował kolejkę.
Na początku zbiór Q jest pusty. Znajdujemy wejście i wyjście. Ponumerujmy kratki tablicy z rysunku: w pionie od 1 do 12 i poziomie od 1 do 10 (kwadracik z numerem 1, czyli wejście, ma wspórzędne [1,1] a 21 -wyjście- [10,12]).
Dołączamy współrzędne wejścia do kolejki, czyli Q={(1,1)}. Następnie przechodzimy do pętli. Pobieramy z początku kolejki współrzędne pewnego punktu, jest to P=(1,1), kolejka jest pusta, Q={}. Sprawdzamy, gdzie możemy iść z punktu P: tylko w dół, a więc dołączamy do kolejki współrzędne punktu pod P, Q={(1,2)} zwiększamy licznik o 1 i przypisujemy jego wartość (czyli 2) tablicy w miejscu (1,2) i przechodzimy na początek pętli. Pobieramy punkt P=(1,2), Q={} i sprawdzamy, gdzie można iść: w dół i w lewo. Dołączamy współrzędne tych dwóch punktów do kolejki, a więc Q={(1,3),{2,2)}, zwiększamy licznik i przypisujemy tym punktom liczbę 3. Znowy na początek pętli, ale tym razem po pobraniu punktu P=(1,3) kolejka nie jest już pusta: Q={(2,2)}. Z punktu P można iść tylko w dół, dołączamy punkt (1,4) do kolejki: Q={(2,2),(1,4)} i przypisujemy tablicy w miejscu (1,4) wartośc licznika po zwiększeniu, czyli 4. Znów na początek pętli i pobieramy P=(2,2), Q={(1,4)}. Z P można iść w prawo, więc dołączamy punkt (2,3) do kolejki: Q={(1,4), (2,3)} i przypisujemy punktowi (2,2) liczbę 4 i dopiero teraz zwiększamy licznik do 5. Postępujemy tak dalej aż dojdziemy do momentu, w którym pobrany z kolejki punkt P będzie miał współrzędne (10,12).
Na rysunku kolor żólty oznacza rozwidlenia a zielony- miejsca z których nie można już nigdzie iść. Gdy dojdziemy do wyjścia zmienna licznik będzie zawierała najkrótszą odległość od wejścia (u nas 21).

Przeanalizujmy teraz kilka kroków algorytmu dla labiryntu z powyższego rysunku.
Przypisujemy zmiennej licznik wartość 1. Niech Q będzie zbiorem par liczb- współrzędnych punktów. Zbiór Q będzie symbolizował kolejkę.
Na początku zbiór Q jest pusty. Znajdujemy wejście i wyjście. Ponumerujmy kratki tablicy z rysunku: w pionie od 1 do 12 i poziomie od 1 do 10 (kwadracik z numerem 1, czyli wejście, ma wspórzędne [1,1] a 21 -wyjście- [10,12]).
Dołączamy współrzędne wejścia do kolejki, czyli Q={(1,1)}. Następnie przechodzimy do pętli. Pobieramy z początku kolejki współrzędne pewnego punktu, jest to P=(1,1), kolejka jest pusta, Q={}. Sprawdzamy, gdzie możemy iść z punktu P: tylko w dół, a więc dołączamy do kolejki współrzędne punktu pod P, Q={(1,2)} zwiększamy licznik o 1 i przypisujemy jego wartość (czyli 2) tablicy w miejscu (1,2) i przechodzimy na początek pętli. Pobieramy punkt P=(1,2), Q={} i sprawdzamy, gdzie można iść: w dół i w lewo. Dołączamy współrzędne tych dwóch punktów do kolejki, a więc Q={(1,3),{2,2)}, zwiększamy licznik i przypisujemy tym punktom liczbę 3. Znowy na początek pętli, ale tym razem po pobraniu punktu P=(1,3) kolejka nie jest już pusta: Q={(2,2)}. Z punktu P można iść tylko w dół, dołączamy punkt (1,4) do kolejki: Q={(2,2),(1,4)} i przypisujemy tablicy w miejscu (1,4) wartośc licznika po zwiększeniu, czyli 4. Znów na początek pętli i pobieramy P=(2,2), Q={(1,4)}. Z P można iść w prawo, więc dołączamy punkt (2,3) do kolejki: Q={(1,4), (2,3)} i przypisujemy punktowi (2,2) liczbę 4 i dopiero teraz zwiększamy licznik do 5. Postępujemy tak dalej aż dojdziemy do momentu, w którym pobrany z kolejki punkt P będzie miał współrzędne (10,12).
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Jakub Konieczny | C/C++ | skanowanie całej mapy | .cpp | .cpp | ***** / 8 |
| Michał Knasiecki | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 1 |
Poprawiony: 01 września 2015 09:11



Bardzo ciekawe, ja niestety mam inny problem, bo muszę znaleźć drogę w labiryncie trójkątnym, jest z niego tylko jedna droga wyjścia, najpierw go muszę wygenerować jak reprezentować labirynt trójkątny w strukturze danych?
Prubowałem zmienić pętle z
for I := 1 to 10 do
na
for I := 1 to 20 do
Ale wyskoczył błąd przy funkcje Gdzie iść.