Wpisany przez Michał Walenciak,
23 sierpnia 2006 19:32
Problem 8 hetmanów polega na ustawieniu na szachownicy tychże figur tak, aby żadna z nich nie mogła zabić innej. Królowa, zwana hetmanem, ustawiona na szachownicy atakuje wszystkie pola w poziomie, w pionie i po skosie. Problem ten został sformułowany przez J.C. Gaussa w 1850 roku. Oto przykład jednego z 92 możliwych rozwiązań:
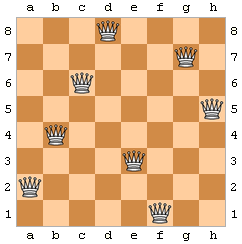
Aby rozwiązać to zadanie można posłużyć się poniższym algorytmem:
Stawiamy hetmana w pierwszym wierszu w pierwszej kolumnie.
Przechodzimy do drugiego wiersza i szukamy pierwszej, wolnej kolumny - w tym wypadku będzie to kolumna trzecia (1. kolumna jest zajęta ze względu na to, iż w pierwszym wierszu już stoi na niej hetman, a 2. gdyż hetman z pierwszego wiersza "patrzy" na nią po przekątnej). Ilustruje to poniższy diagram:

Podobnie postępujemy z kolejnymi wierszami.
W momencie, gdy któregoś hetmana nie da się postawić, (w każdej z 8 kolumn hetman będzie atakowany) to cofamy się o jeden wiersz i przesuwanmy hetmana na kolejne wolne pole. Jeśli takie nie istnieje, to znowu się cofamy itd. Ta cecha sprawia, że algorytm ustawiający hetmany na szachownicy jest przykładem rekurencji z powrotami.
Gdy udało się szczęśliwie postawić 8. hetmana oznacza to, że znaleźliśmy rozwiązanie (zapisujemy ustawienia wszystkich hetmnanów np. w pliku wynikowym).
Jeśli okaże się, że hetmana z pierwszego wiersza nie ma już gdzie postawić, to znaczy, że wszystkie możliwe kombinacje zostały już sprawdzone.
Aby zaimplementować powyższy algorytm w programie, należy ustalić sposób przetrzymywania zajętych już kolumn oraz przekątnych.
O ile z kolumnami nie ma większego problemu (wystarczy stworzyć tablicę [1..8] of boolean i zajęte kolumny oznaczać przez true a wolne przez false) to trochę trudniej jest z przekątnymi.
Jeśli przyjrzymy się szachownicy, to możemy dostrzec, że dla danej przekątnej prawej (np. A1 - H8) różnica numeru kolumny i wiersza (dla pola e4: e jest piątą kolmuną więc 5-4=1) jest stała i przyjmuje wartości od -7 dla "przekątnej" A8 - A8 przez 0 dla A1 - H8 do 7 dla "przekątnej" H1 - H1.
Dla przekątnych lewych z kolei suma numeru kolumny i wiersza jest stała: od 2 dla "przekątnej" A1 - A1 przez 9 dla H1 - A8 do 16 dla H8 - H8.
Oczywiście coś takiego, jak przekątna A1 - A1 czy H1 - H1 nie istnieje, ale nie zaszkodzi sprawdzanie lewej przekątnej w polach A1 i H8, czy prawej w H1 i A8, gdyż pominięcie tej czynności skompilkowało by odrobinę program.
Mała uwaga odnośnie przekątnych: w programie, do zapisywania użytych przekątnych użyłem tablic. Jak wiadomo w większosci języków programowania wartości indeksów tablic muszą być liczbami nie ujemnymi. Dlatego wartości różnic bądź sum numerów kolumn i wierszy powiększam o 128, aby wartości te zawsze były dodatnie i by każdy mógł zmodyfikować program tak, aby poszerzyć problem 8 hetmanów na szachwnicy 8 na 8 do problemu X hetmanów na szachownicy X na X :).

Aby rozwiązać to zadanie można posłużyć się poniższym algorytmem:
Stawiamy hetmana w pierwszym wierszu w pierwszej kolumnie.
Przechodzimy do drugiego wiersza i szukamy pierwszej, wolnej kolumny - w tym wypadku będzie to kolumna trzecia (1. kolumna jest zajęta ze względu na to, iż w pierwszym wierszu już stoi na niej hetman, a 2. gdyż hetman z pierwszego wiersza "patrzy" na nią po przekątnej). Ilustruje to poniższy diagram:

Podobnie postępujemy z kolejnymi wierszami.
W momencie, gdy któregoś hetmana nie da się postawić, (w każdej z 8 kolumn hetman będzie atakowany) to cofamy się o jeden wiersz i przesuwanmy hetmana na kolejne wolne pole. Jeśli takie nie istnieje, to znowu się cofamy itd. Ta cecha sprawia, że algorytm ustawiający hetmany na szachownicy jest przykładem rekurencji z powrotami.
Gdy udało się szczęśliwie postawić 8. hetmana oznacza to, że znaleźliśmy rozwiązanie (zapisujemy ustawienia wszystkich hetmnanów np. w pliku wynikowym).
Jeśli okaże się, że hetmana z pierwszego wiersza nie ma już gdzie postawić, to znaczy, że wszystkie możliwe kombinacje zostały już sprawdzone.
Aby zaimplementować powyższy algorytm w programie, należy ustalić sposób przetrzymywania zajętych już kolumn oraz przekątnych.
O ile z kolumnami nie ma większego problemu (wystarczy stworzyć tablicę [1..8] of boolean i zajęte kolumny oznaczać przez true a wolne przez false) to trochę trudniej jest z przekątnymi.
Jeśli przyjrzymy się szachownicy, to możemy dostrzec, że dla danej przekątnej prawej (np. A1 - H8) różnica numeru kolumny i wiersza (dla pola e4: e jest piątą kolmuną więc 5-4=1) jest stała i przyjmuje wartości od -7 dla "przekątnej" A8 - A8 przez 0 dla A1 - H8 do 7 dla "przekątnej" H1 - H1.
Dla przekątnych lewych z kolei suma numeru kolumny i wiersza jest stała: od 2 dla "przekątnej" A1 - A1 przez 9 dla H1 - A8 do 16 dla H8 - H8.
Oczywiście coś takiego, jak przekątna A1 - A1 czy H1 - H1 nie istnieje, ale nie zaszkodzi sprawdzanie lewej przekątnej w polach A1 i H8, czy prawej w H1 i A8, gdyż pominięcie tej czynności skompilkowało by odrobinę program.
Mała uwaga odnośnie przekątnych: w programie, do zapisywania użytych przekątnych użyłem tablic. Jak wiadomo w większosci języków programowania wartości indeksów tablic muszą być liczbami nie ujemnymi. Dlatego wartości różnic bądź sum numerów kolumn i wierszy powiększam o 128, aby wartości te zawsze były dodatnie i by każdy mógł zmodyfikować program tak, aby poszerzyć problem 8 hetmanów na szachwnicy 8 na 8 do problemu X hetmanów na szachownicy X na X :).
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C/C++ | .cpp | .cpp | ***** / 12 | |
| Michał Walenciak | Delphi/Pascal | .pas | .pas | ***** / 4 | |
| Tomasz Lubiński | Java | .java | .java | ***** / 1 |
Poprawiony: 14 sierpnia 2012 21:40
Komentarze
+3
#
drocos
2009-10-30 00:50
świetny algorytm
Odpowiedz | Odpowiedz z cytatem | Cytować
+9
#
Henryk
2010-01-18 14:01
Dziękję za pomoc w problemie ośmiu hetmanów dla pascala Pozdrowienia dla wszystkich których znasz i kochasz
Odpowiedz | Odpowiedz z cytatem | Cytować
+5
#
michu
2012-03-05 22:42
super portal! świetna treść:) takich ludzi potrzebujemy!!!
Odpowiedz | Odpowiedz z cytatem | Cytować
+6
#
Igalb
2012-04-26 15:44
Świetne! Dziękujemy za wytłumaczenie i udostępnienie!
Odpowiedz | Odpowiedz z cytatem | Cytować
Dodaj komentarz


