Wpisany przez Adam Mika,
25 sierpnia 2008 20:53
Czym jest skoczek (konik) szachowy?
Skoczek, zwany inaczej konikiem jest jedną z figur w szachach.
Dopuszczalne ruchy skoczka:
Jeden ruch konika to skok o dwa pola w pionie bądź poziomie a następnie o jedno pole pod kątem prostym. Ruch taki tworzy literę "L". Wszystkie dopuszczalne ruchy skoczka pokazane są na schemacie poniżej:
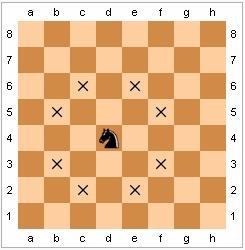
Istota problemu:
Ruszając z wyznaczonego pola na szachownicy (problem klasyczny – pole a1) poruszając się zgodnie z regułą ruchu skoczka należy odwiedzić wszystkie pola szachownicy tak aby każde pole zostało odwiedzone dokładnie jeden raz. Odwiedzając kolejne pola skoczek numeruje je. W wersji klasycznej problemu mamy do czynienia z szachownicą 8x8 nic nie stoi jednak na przeszkodzie, aby rozważać dowolną tablicę n x n (n- liczba naturalna dodatnia).
Czego oczekujemy w wyniku?
Tablica liczb reprezentująca ruchy skoczka. Jako rozwiązanie problemu możemy uzyskać kilka różnych tablic liczb. Możemy również odnaleźć tylko jedno rozwiązanie (szukamy do pierwszego rozwiązania).
Jak rozwiązać problem?
Nie są znane algorytmy które umożliwiałyby odnalezienie poprawnego rozwiązania w inny sposób niż sprawdzenie (wszystkich) możliwych zestawów ruchów skoczka. Każdy zestaw ruchów albo jest rozwiązaniem problemu albo prowadzi do blokady skoczka (brak możliwości wykonania kolejnego ruchu przy czym nie wszystkie pola zostały jeszcze odwiedzone).
Przykłady:
Algorytm:
Do rozwiązania tego problemu stosuje się rekurencyjny algorytm z powrotami. Ideę tego algorytmu przedstawia poniższy pseudokod:
W przypadku problemu skoczka algorytm ten będzie wyglądał następująco:
Jak to działa?
Skoczek z bieżącego pola (które zawsze na początku numeruje) próbuje przejść na kolejne pole. Jeśli może to uczynić to skacze – wtedy też wywoływana jest rekurencja, gdyż mamy do czynienia z takim samym problemem jednak o powiększonym zbiorze pól odwiedzonych. Jeśli natomiast nie jest dopuszczalny dany wariant ruchu konik usiłuje wykonać kolejny wariant. Jeśli żaden z dopuszczalnych wariantów ruchu nie może zostać wykonany konik wie, że ta droga nie prowadzi do celu, dlatego też wycofuje się z ostatnio wykonanego ruchu. Dodatkowo po powrocie z rekurencyjnego wywołania funkcji sprawdzamy czy znaleziono już rozwiązanie - wyjście z funkcji w takim wypadku powoduje, że kończymy obliczenia po znalezieniu pierwszego rozwiązania, jeżeli usuniemy ten warunek wówczas szukać będziemy wszystkich możliwych rozwiązań problemu.
Złożoność algorytmu:
Dla algorytmu w przedstawionej wersji: O(n!).
Wymagane struktury danych:
Tablica, której elementami są liczby odpowiadające zbiorowi liczb naturalnych {0, ..., n*n}, np. int, shot, byte, itp. Tablica ta reprezentuje szachownicę wraz z zaznaczonymi na niej ruchami skoczka.
Możliwe optymalizacje/modyfikacje:
Skoczek, zwany inaczej konikiem jest jedną z figur w szachach.
Dopuszczalne ruchy skoczka:
Jeden ruch konika to skok o dwa pola w pionie bądź poziomie a następnie o jedno pole pod kątem prostym. Ruch taki tworzy literę "L". Wszystkie dopuszczalne ruchy skoczka pokazane są na schemacie poniżej:

Istota problemu:
Ruszając z wyznaczonego pola na szachownicy (problem klasyczny – pole a1) poruszając się zgodnie z regułą ruchu skoczka należy odwiedzić wszystkie pola szachownicy tak aby każde pole zostało odwiedzone dokładnie jeden raz. Odwiedzając kolejne pola skoczek numeruje je. W wersji klasycznej problemu mamy do czynienia z szachownicą 8x8 nic nie stoi jednak na przeszkodzie, aby rozważać dowolną tablicę n x n (n- liczba naturalna dodatnia).
Czego oczekujemy w wyniku?
Tablica liczb reprezentująca ruchy skoczka. Jako rozwiązanie problemu możemy uzyskać kilka różnych tablic liczb. Możemy również odnaleźć tylko jedno rozwiązanie (szukamy do pierwszego rozwiązania).
Jak rozwiązać problem?
Nie są znane algorytmy które umożliwiałyby odnalezienie poprawnego rozwiązania w inny sposób niż sprawdzenie (wszystkich) możliwych zestawów ruchów skoczka. Każdy zestaw ruchów albo jest rozwiązaniem problemu albo prowadzi do blokady skoczka (brak możliwości wykonania kolejnego ruchu przy czym nie wszystkie pola zostały jeszcze odwiedzone).
Przykłady:
- Dla szachownicy 3x3 nie istnieje rozwiązanie (nie odwiedzimy "środkowego" pola)
- Dla szachownicy 5x5:
- Pewne sekwencje ruchów prowadzą do blokady, np. startując z pola b5:
1 12 17 6 13 18 7 11 8 2 5 16 3 14 19 10 9 4 15 20 - Inne natomiast mogą prowadzić do rozwiązania problemu, np. startując z pola a5
1 20 17 12 3 16 11 2 7 18 21 24 19 4 13 10 15 6 23 8 25 22 9 14 5
- Pewne sekwencje ruchów prowadzą do blokady, np. startując z pola b5:
Algorytm:
Do rozwiązania tego problemu stosuje się rekurencyjny algorytm z powrotami. Ideę tego algorytmu przedstawia poniższy pseudokod:
if koniec?
wypisz_wynik()
else
for each dopuszczalna_operacja
if można_wynokać_operacje?
wykonaj_operacje() // rekurencyjnie
end
end
cofnij_ostatnio_wykonaną_operacje()
end
W przypadku problemu skoczka algorytm ten będzie wyglądał następująco:
numeruj_bieżące_pole()
if nr_skoku == n*n
wypisz_tablice_liczb()
else
for each wariant_ruchu (i = 1,...,8)
if można_wynokać_wariant_skoku_nr_i?
skocz(...) // rekurencyjnie
if znaleziono rozwiązanie
return;
end
end
oznacz_bieżące_pole_w_tablicy_jako_nieodwiedzone()
end
Jak to działa?
Skoczek z bieżącego pola (które zawsze na początku numeruje) próbuje przejść na kolejne pole. Jeśli może to uczynić to skacze – wtedy też wywoływana jest rekurencja, gdyż mamy do czynienia z takim samym problemem jednak o powiększonym zbiorze pól odwiedzonych. Jeśli natomiast nie jest dopuszczalny dany wariant ruchu konik usiłuje wykonać kolejny wariant. Jeśli żaden z dopuszczalnych wariantów ruchu nie może zostać wykonany konik wie, że ta droga nie prowadzi do celu, dlatego też wycofuje się z ostatnio wykonanego ruchu. Dodatkowo po powrocie z rekurencyjnego wywołania funkcji sprawdzamy czy znaleziono już rozwiązanie - wyjście z funkcji w takim wypadku powoduje, że kończymy obliczenia po znalezieniu pierwszego rozwiązania, jeżeli usuniemy ten warunek wówczas szukać będziemy wszystkich możliwych rozwiązań problemu.
Złożoność algorytmu:
Dla algorytmu w przedstawionej wersji: O(n!).
Wymagane struktury danych:
Tablica, której elementami są liczby odpowiadające zbiorowi liczb naturalnych {0, ..., n*n}, np. int, shot, byte, itp. Tablica ta reprezentuje szachownicę wraz z zaznaczonymi na niej ruchami skoczka.
Możliwe optymalizacje/modyfikacje:
- Możemy wypisać wszystkie (różne) dopuszczalne rozwiązania problemu
- Pewne pola na szachownicy są na początku odgórnie niedopuszczalne
- Szachownica o rozmiarze różnym od 8
- Punkt początkowy skoczka
- Przed wykonaniem kolejnego ruchu (wywołanie rekurencyjne) na podstawie poprzednich ruchów wpływamy na wybór kolejnego ruchu (idea powstała jako próba zmniejszenia złożoności algorytmu)
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C# | MS Visual Studio .net | .cs | .cs | ***** / 3 |
| Adam Mika | C/C++ | .cpp | .cpp | ***** / 13 | |
| Tomasz Lubiński | Delphi/Pascal | .pas | .pas | ***** / 4 | |
| Tomasz Lubiński | Java | .java | .java | ***** / 4 | |
| foxbond | Php | .php | .php | ***** / 0 | |
| Jakub Burzynski | Python | Python 2.7.2 | .py | .py | ***** / 4 |
Poprawiony: 26 sierpnia 2015 13:44


