Wpisany przez Michał Witaszek,
17 czerwca 2011 13:24
Problem wydawania reszty polega na podzieleniu wartości (reszty do wydania) na jak najmniejszą liczbę elementów. Czyli na wydaniu reszty przy pomocy najmniejszej możliwej liczby banknotów/bilonów. By wydać resztę musimy najpierw ustalić listę dostępnych nominałów. Niech będzie to tablica N o wartościach {200, 100, 50, 20, 10, 5, 2, 1}
Problem ten daje się rozwiązać przy pomocy metody zachłannej, czyli do wypłacania reszty będziemy zawsze używać największych dostępnych nominałów. Oczywiście użyty nominał musi być mniejszy lub równy wydawanej wartości.
Najłatwiej znaleźć rozwiązanie, gdy tablicę dostępnych nominałów posortujemy malejąco. A więc, najpierw szukamy wartości mniejszej lub równej wypłacanej kwocie. Po znalezieniu jej używamy największej możliwej ilości znalezionego nominału. Tą liczbą jest wynik dzielenia bez reszty wypłacanej kwoty przez wartość odnalezionego nominału. Resztę do wydania należy zmniejszyć o kwotę wypłaconą za pomocą bieżącego nominału. I powtórzyć szukanie. Czynność tą powtarzamy tak długo aż wypłacimy całą sumę.
Schemat postępowania można przedstawić za pomocą następującego schematu blokowego:
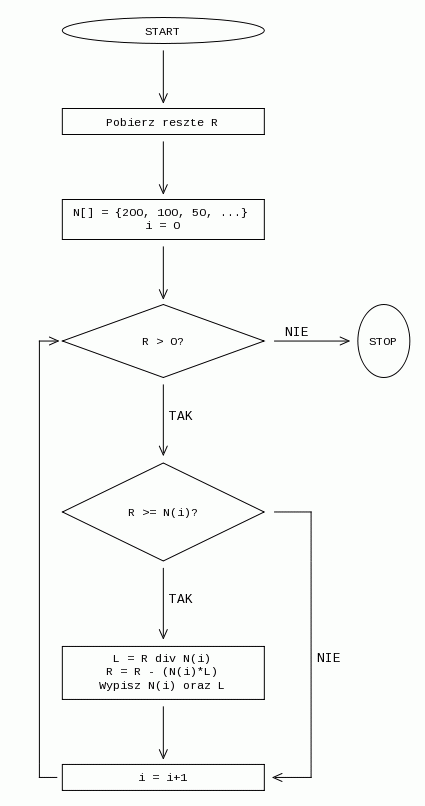
Przyjmijmy dostępne nominały (200, 100, 50, 20, 10, 5, 2, 1) PLN.
Załóżmy że chcemy wypłacić kwotę 148 PLN.
Największym nominałem nie większym niż 148 jest 100.
148 div 100 = 1 Wypłacamy jeden banknot 100 PLN.
148 – (100*1) = 48, zostało nam jeszcze do wydania 48 PLN.
Kolejną wartością nie większą niż aktualna reszta jest 20.
48 div 20 = 2 Wypłacamy dwa banknoty 20 PLN.
48 – (20*2) = 8, zostało nam jeszcze do wydania 8 PLN.
Największy nominał nie większy niż 8 to 5 PLN
8 div 5 =1 Wypłacamy monetę 5 PLN
8 – 5 = 3, zostało nam jeszcze do wydania 3 PLN.
Wartość nie większa niż 3 to 2
3 div 2 = 1 Jedna moneta 2 PLN
3 – 2 = 1
Do wydania pozostaje już tylko złotówka
1 – 1 = 0
Reszta została wydana za pomocą nominałów:
100*1 + 20*2 + 5*1 + 2*1 + 1*1 = 148
Przyjmijmy teraz, że mamy również do dyspozycji grosze. Zatem tablica naszych nominałów wyglądać będzie teraz następująco: (200, 100, 50, 20, 10, 5, 2, 1, 0.50, 0.20, 0.10, 0.05, 0.02, 0.01) PLN.
Załóżmy że chcemy wypłacić kwotę 12.45 PLN.
Największym nominałem nie większym niż 12.45 jest 10.
12.45 / 10 = 1.245, bez reszty to 1, a więc Wypłacamy jeden banknot 10 PLN.
12.45 – (10*1) = 2.45.
Teraz największym nominałem nie większym niż 2.45 jest 2.
2.45 / 2 = 1.225, bez reszty to 1, a więc Wypłacamy jedną monetę 2 PLN.
2.45 – (2*1) = 0.45
Zostało nam więc do wypłacenia jeszcze 45 groszy, największy możliwy nominał to 0.20 czyli 20 groszy.
0.45 / 0.20 = 2.25, bez reszty to 2, zatem wypłacamy 2 monety 20 groszowe.
0.45 - (0.20*.) = 0.05
Do wydania pozostaje już tylko 5 groszy
0.05 – 0.05 = 0
Reszta została wydana za pomocą nominałów:
10*1 + 2*1 + 0.20*2 + 0.05*1 = 12.45
Problem ten daje się rozwiązać przy pomocy metody zachłannej, czyli do wypłacania reszty będziemy zawsze używać największych dostępnych nominałów. Oczywiście użyty nominał musi być mniejszy lub równy wydawanej wartości.
Najłatwiej znaleźć rozwiązanie, gdy tablicę dostępnych nominałów posortujemy malejąco. A więc, najpierw szukamy wartości mniejszej lub równej wypłacanej kwocie. Po znalezieniu jej używamy największej możliwej ilości znalezionego nominału. Tą liczbą jest wynik dzielenia bez reszty wypłacanej kwoty przez wartość odnalezionego nominału. Resztę do wydania należy zmniejszyć o kwotę wypłaconą za pomocą bieżącego nominału. I powtórzyć szukanie. Czynność tą powtarzamy tak długo aż wypłacimy całą sumę.
Schemat postępowania można przedstawić za pomocą następującego schematu blokowego:

Przykład:
Przyjmijmy dostępne nominały (200, 100, 50, 20, 10, 5, 2, 1) PLN.
Załóżmy że chcemy wypłacić kwotę 148 PLN.
Największym nominałem nie większym niż 148 jest 100.
148 div 100 = 1 Wypłacamy jeden banknot 100 PLN.
148 – (100*1) = 48, zostało nam jeszcze do wydania 48 PLN.
Kolejną wartością nie większą niż aktualna reszta jest 20.
48 div 20 = 2 Wypłacamy dwa banknoty 20 PLN.
48 – (20*2) = 8, zostało nam jeszcze do wydania 8 PLN.
Największy nominał nie większy niż 8 to 5 PLN
8 div 5 =1 Wypłacamy monetę 5 PLN
8 – 5 = 3, zostało nam jeszcze do wydania 3 PLN.
Wartość nie większa niż 3 to 2
3 div 2 = 1 Jedna moneta 2 PLN
3 – 2 = 1
Do wydania pozostaje już tylko złotówka
1 – 1 = 0
Reszta została wydana za pomocą nominałów:
100*1 + 20*2 + 5*1 + 2*1 + 1*1 = 148
Przyjmijmy teraz, że mamy również do dyspozycji grosze. Zatem tablica naszych nominałów wyglądać będzie teraz następująco: (200, 100, 50, 20, 10, 5, 2, 1, 0.50, 0.20, 0.10, 0.05, 0.02, 0.01) PLN.
Załóżmy że chcemy wypłacić kwotę 12.45 PLN.
Największym nominałem nie większym niż 12.45 jest 10.
12.45 / 10 = 1.245, bez reszty to 1, a więc Wypłacamy jeden banknot 10 PLN.
12.45 – (10*1) = 2.45.
Teraz największym nominałem nie większym niż 2.45 jest 2.
2.45 / 2 = 1.225, bez reszty to 1, a więc Wypłacamy jedną monetę 2 PLN.
2.45 – (2*1) = 0.45
Zostało nam więc do wypłacenia jeszcze 45 groszy, największy możliwy nominał to 0.20 czyli 20 groszy.
0.45 / 0.20 = 2.25, bez reszty to 2, zatem wypłacamy 2 monety 20 groszowe.
0.45 - (0.20*.) = 0.05
Do wydania pozostaje już tylko 5 groszy
0.05 – 0.05 = 0
Reszta została wydana za pomocą nominałów:
10*1 + 2*1 + 0.20*2 + 0.05*1 = 12.45
Przykład w JavaScript:
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Jacek Gzel | C# | .cs | .cs | ***** / 5 | |
| Michał Witaszek | C/C++ | .cpp | .cpp | ***** / 68 | |
| Michał Witaszek | Delphi/Pascal | .pas | .pas | ***** / 2 | |
| Dominik Goździuk | Java | .java | .java | ***** / 3 | |
| Tomasz Lubiński | JavaScript | .js | .js | ***** / 7 |
Poprawiony: 15 sierpnia 2012 09:49



Oczywiście system monetarny jest tak dobrany, by spełniał warunek ai mniejsze bądź równe a(i+1)/2
1 x 483,
117 x 1.
Algorytm zachłanny działa tu prawidłowo gdy nominały posortowane malejąco spełniają warunek: ai mniejsze bądź równe a(i+1)/2.
Podane w artykule nominaly spełniają ten warunek. Powyższe nie spełniają.