Wpisany przez Tomasz Nędza,
28 lipca 2005 22:51
Ciekawym rodzajem drzewa jest drzewo BSP. Jest to rozwinięcie pomysłu wykorzystanego w drzewie BST - całość działa na prawie identycznych zasadach. Pomimo, że wymaga na początku bardzo czasochłonnego budowania, jest to wydajna metoda obliczania zależności widoczności wśród grupy wielokątów 3D oglądanych z dowolnego punktu na scenie. Za każdym razem, gdy zmienia się położenie obserwatora, wykonywany jest liniowy algorytm wyświetlania. Łatwo zauważyć po złożoności poszczególnych części algorytmu, że metoda ta dobrze nadaje się do zastosowań, w których zmienia się punkt obserwacji, natomiast same obiekty pozostają niezmienne.
Pierwsza część algorytmu polega na zbudowaniu drzewa binarnego ścian składających się na scenę. W korzeniu tego drzewa umieszczany jest dowolny wielokąt ze sceny. Dla prawidłowości algorytmu nie ma znaczenia, który wielokąt wybierzemy. Za pomocą tego wielokąta (a raczej za pomocą płaszczyzny, na której ten wielokąt się znajduje) następuje podział pozostałych ścian na dwie grupy, w zależności od tego, w której półprzestrzeni się znajdują. Do pierwszej półprzestrzeni należą wszystkie pozostałe wielokąty znajdujące się przed wielokątem z korzenia, a druga zawiera wielokąty leżące za wielokątem korzenia. Niektóre wielokąty (znajdujące się jednocześnie w obu półprzestrzeniach) muszą być podzielone przez wspomnianą płaszczyznę, a następnie ich części są przypisywane do odpowiednich grup. Dla każdej grupy powtarzamy dotychczasowe kroki algorytmu, to znaczy wybieramy wielokąt do korzenia (staje się on przednim albo tylnym potomkiem) i dzielimy pozostałe ściany. Algorytm budowy drzewa BSP kończy się, gdy każdy węzeł zawiera tylko jeden wielokąt.
Myślę, że najłatwiej będzie to zrozumieć na przykładzie.
Przypuśćmy, że dany mamy następujący zestaw ścian (rzut z góry):
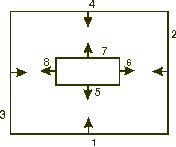
Strzałki przy ścianach oznaczają ich normalne, czyli kierunek, z którego płaszczyzna może być oglądana. Łatwo spostrzec, że rzut przedstawia pomieszczenie z dużym filarem. Liczby oznaczają numery danych ścian (za ich pomocą będziemy przedstawiać je w drzewie BSP). Na rysunku tym widać sytuację, o której już wspomniałem - nie zawsze można odpowiedzieć na pytanie, po której stronie danej ściany leży inna ściana. Gdy wybierzemy na przykład ścianę numer 5, nie będziemy mogli powiedzieć, czy ściana 2 leży z przodu czy też z tyłu. W zasadzie leży po obu stronach. W tym przypadku należy podzielić problematyczną ścianę na dwie części. Aby budowę drzewa BSP bardziej upodobnić do tworzenia drzewa BST, trochę zmienię sposób postępowania. Będę brał po jednej ścianie i wstawiał w odpowiednie miejsce drzewa BSP. W sumie jednak otrzymamy równoważne drzewo. Zacznijmy więc budowanie. Pierwszą ścianą do wstawienia niech będzie na przykład ściana 5. Jako że drzewo jest puste, wstawiamy tę ścianę do korzenia.
Dla ułatwienia przy "wskaźnikach" umieszczę nazwę półprzestrzeni, jaka jest wskazywana.
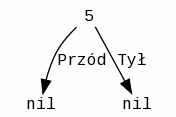
Kolejną wstawianą ścianą będzie ściana nr 1. Z rysunku widać, że cała jest w "przedniej" półprzestrzeni względem ściany 5, więc umieścimy ją jako jej lewego potomka.
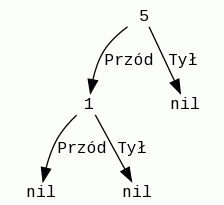
Teraz chcę wstawić ścianę nr 3. Ścianę tą będę musiał podzielić, gdyż znajduje się i z przodu, i z tyłu względem ściany 5. Podobnie zrobię od razu ze ścianą nr 2.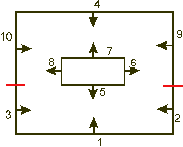
Czerwonymi kreskami oznaczę miejsca podziału ścian. W wyniku tego działania otrzymałem nowe ściany: 3, 10, 9 oraz 2. Wstawię je teraz do drzewa. Ściana nr 3 jest z przodu ściany nr 5 oraz z przodu ściany nr 1, więc znajdzie się w lewym poddrzewie węzła 1. To samo robię ze ścianą nr 2. Schemat otrzymanego drzewa znajduje się po lewej.
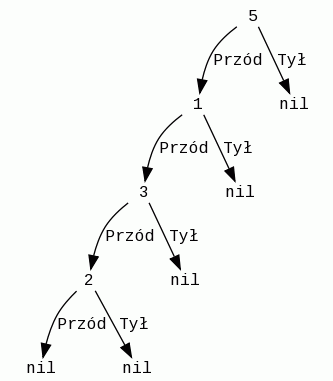
Do zbadania pozostały nam jeszcze ściany 10, 4, 9, 8, 7 i 6. Wstawmy ścianę nr 7. Znajduje się ona z tyłu ściany nr 5. Trafi więc do prawego poddrzewa. Ściana nr 6 także trafi do prawego poddrzewa względem głównego korzenia, ale po porównaniu ze ścianą nr 7 (pamiętajmy, że ona tam się już znajduje) okaże się, że nr 6 będzie jej prawym potomkiem. Wstawmy teraz ścianę numer 8, a następnie ścianę nr 4.
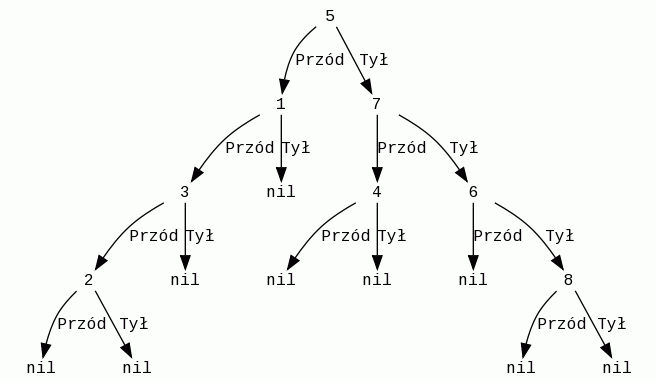
Problem pojawi się przy ścianach nr 9 i 10, ale wystarczy je podzielić w pokazany sposób i wstawienie ich do drzewa nie powinno sprawić trudności.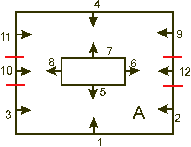
Końcowa postać drzewa prezentuje się następująco (schemat poniżej):
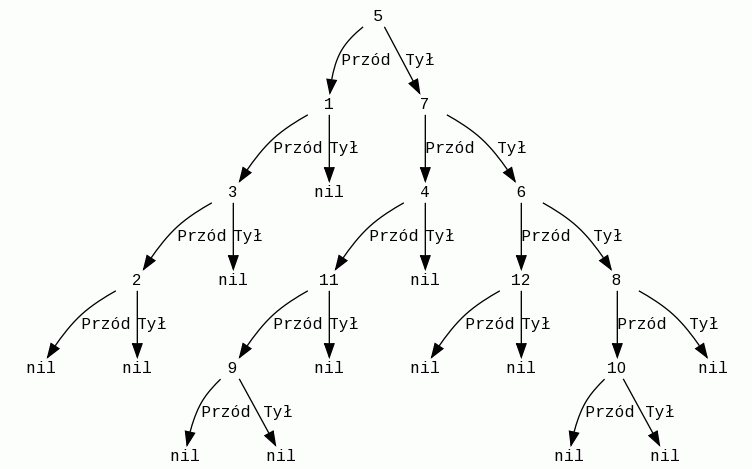
Drzewo to jest kluczem do prawidłowego posortowania naszych ścian podczas rysowania. Jeżeli obserwator znajduje się przed ścianą znajdującą się w korzeniu (w półprzestrzeni wskazywanej przez jej wektor normalny), to wyświetlanie należy rozpocząć od ścian z tylnej półprzestrzeni. Znajdują się w niej przecież ściany, które mogą być zasłonięte na ekranie przez wielokąt z korzenia. Następnie należy oczywiście wyświetlić ścianę znajdującą się w korzeniu, a na końcu wszystkie wielokąty leżące przed tą ścianą. W przypadku gdy obserwator jest w tylnej półprzestrzeni, najpierw trzeba wyświetlić wszystkie wielokąty z przedniej półprzestrzeni korzenia, potem wielokąt znajdujący się w korzeniu i wreszcie wszystkie wielokąty w jego tylnej półprzestrzeni. Załóżmy, że obserwator znajduje się w punkcie A. Jego pozycję testujemy względem położenia ścian według poniższego algorytmu:

Strzałki przy ścianach oznaczają ich normalne, czyli kierunek, z którego płaszczyzna może być oglądana. Łatwo spostrzec, że rzut przedstawia pomieszczenie z dużym filarem. Liczby oznaczają numery danych ścian (za ich pomocą będziemy przedstawiać je w drzewie BSP). Na rysunku tym widać sytuację, o której już wspomniałem - nie zawsze można odpowiedzieć na pytanie, po której stronie danej ściany leży inna ściana. Gdy wybierzemy na przykład ścianę numer 5, nie będziemy mogli powiedzieć, czy ściana 2 leży z przodu czy też z tyłu. W zasadzie leży po obu stronach. W tym przypadku należy podzielić problematyczną ścianę na dwie części. Aby budowę drzewa BSP bardziej upodobnić do tworzenia drzewa BST, trochę zmienię sposób postępowania. Będę brał po jednej ścianie i wstawiał w odpowiednie miejsce drzewa BSP. W sumie jednak otrzymamy równoważne drzewo. Zacznijmy więc budowanie. Pierwszą ścianą do wstawienia niech będzie na przykład ściana 5. Jako że drzewo jest puste, wstawiamy tę ścianę do korzenia.
Dla ułatwienia przy "wskaźnikach" umieszczę nazwę półprzestrzeni, jaka jest wskazywana.

Kolejną wstawianą ścianą będzie ściana nr 1. Z rysunku widać, że cała jest w "przedniej" półprzestrzeni względem ściany 5, więc umieścimy ją jako jej lewego potomka.

Teraz chcę wstawić ścianę nr 3. Ścianę tą będę musiał podzielić, gdyż znajduje się i z przodu, i z tyłu względem ściany 5. Podobnie zrobię od razu ze ścianą nr 2.

Czerwonymi kreskami oznaczę miejsca podziału ścian. W wyniku tego działania otrzymałem nowe ściany: 3, 10, 9 oraz 2. Wstawię je teraz do drzewa. Ściana nr 3 jest z przodu ściany nr 5 oraz z przodu ściany nr 1, więc znajdzie się w lewym poddrzewie węzła 1. To samo robię ze ścianą nr 2. Schemat otrzymanego drzewa znajduje się po lewej.

Do zbadania pozostały nam jeszcze ściany 10, 4, 9, 8, 7 i 6. Wstawmy ścianę nr 7. Znajduje się ona z tyłu ściany nr 5. Trafi więc do prawego poddrzewa. Ściana nr 6 także trafi do prawego poddrzewa względem głównego korzenia, ale po porównaniu ze ścianą nr 7 (pamiętajmy, że ona tam się już znajduje) okaże się, że nr 6 będzie jej prawym potomkiem. Wstawmy teraz ścianę numer 8, a następnie ścianę nr 4.

Problem pojawi się przy ścianach nr 9 i 10, ale wystarczy je podzielić w pokazany sposób i wstawienie ich do drzewa nie powinno sprawić trudności.

Końcowa postać drzewa prezentuje się następująco (schemat poniżej):

Drzewo to jest kluczem do prawidłowego posortowania naszych ścian podczas rysowania. Jeżeli obserwator znajduje się przed ścianą znajdującą się w korzeniu (w półprzestrzeni wskazywanej przez jej wektor normalny), to wyświetlanie należy rozpocząć od ścian z tylnej półprzestrzeni. Znajdują się w niej przecież ściany, które mogą być zasłonięte na ekranie przez wielokąt z korzenia. Następnie należy oczywiście wyświetlić ścianę znajdującą się w korzeniu, a na końcu wszystkie wielokąty leżące przed tą ścianą. W przypadku gdy obserwator jest w tylnej półprzestrzeni, najpierw trzeba wyświetlić wszystkie wielokąty z przedniej półprzestrzeni korzenia, potem wielokąt znajdujący się w korzeniu i wreszcie wszystkie wielokąty w jego tylnej półprzestrzeni. Załóżmy, że obserwator znajduje się w punkcie A. Jego pozycję testujemy względem położenia ścian według poniższego algorytmu:
- Korzeń zawiera ścianę nr 5. Ponieważ punkt A znajduje się z przodu tej ściany, przechodzimy w drzewie do poddrzewa po prawej.
- Napotykamy na kolejny test. Tym razem względem ściany nr 7. Punkt A znajduje się z tyłu tej ściany, więc wchodzimy w poddrzewo po stronie lewej.
- Znaleźliśmy się w węźle, który posiada jedynie jednego potomka, więc przechodzimy tam bez żadnych testów. W węźle ze ścianą nr 11 powtarzamy tą czynność.
- Znajdujemy się w węźle ze ścianą nr 9. Oba jej wskaźniki mają wartość nil, więc wracamy do pierwszego "rozgałęzienia" w górę, zapamiętując kolejne "mijane" ściany (a więc kolejno: 9, 11, 4, 7).
- Wchodzimy teraz w prawe poddrzewo.
- Znów napotykamy na test. Tym razem chodzi o określenie położenia punktu A względem ściany nr 6. Znajduje się on z przodu tej ściany, a więc wchodzimy w prawe poddrzewo.
- Węzeł ze ścianą nr 8 ma tylko jednego potomka, a więc przechodzimy do ściany nr 10.
- Powracając w górę zapamiętujemy "odwiedzone" ściany (aktualna tablica ścian: 9, 11, 4, 7, 10, 8, 6).
- Z węzła ze ścianą nr 6 przechodzimy w lewe poddrzewo. Jest to pojedyncza ściana, a więc powracamy w górę - do węzła nr 5.
- Przechodzimy do lewej gałęzi. Dochodzimy aż do węzła ze ścianą nr 2, po czym następuje powrót do korzenia.
- Po całym przejściu drzewa otrzymaliśmy następującą kolejność ścian: 9, 11, 4, 7, 10, 8, 6, 12, 5, 2, 3, 1
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
Poprawiony: 30 sierpnia 2012 14:31


