Wpisany przez Michał Knasiecki,
16 sierpnia 2005 19:23
Drzewo BST (binary search tree) jest drzewem binarnym. Oprócz pola wartości drzewo BST posiada jeszcze dwa pola:
L i P, wskazujące odpowiednio na lewy i prawy następnik. Drzewo BST ma szczególną własność:
Jeśli drzewo BST jest puste (korzeń=nil) należy wstawić element (nie porównujemy go z innymi), w przeciwnym wypadku porównujemy wartość elementu z następnikami każdego węzła (zaczynając od korzenia). Jeżeli wartość elementu jest niewiększa od wartości porównywanego wierzchołka to przechodzimy do lewego następnika, w przeciwnym razie przechodzimy do prawego następnika. Krok ten powtarzamy aż znajdziemy dla naszego elementu odpowiedznie miejsce, tzn. gdy następnik, do którego powinniśmy iść jest pusty (nil). Następnie wstawiamy element jako odpowiedni następnik (prawy, jeśli element jest większy od węzła, lewy jeśli niewiększy).
Usuwanie elementów:
Jeżeli usuwany element nie ma następników to można zwolnić przydzieloną mu pamięć. Jeśli element do usunięcia ma jeden następnik należy go połączyć (następnik) z poprzednikiem usuwanego elementu. Jeśli element ma dwa następniki można go usunąć na dwa sposoby:
Można to zrobić na dwa sposoby: od końca, schodząc za każdym razem od korzenia lub od korzenia. Ta druga metoda jest znacznie szybsza, wymaga jednak zastosowania stosu, na którym umieszczamy następniki usuwanego elementu. Po usunięciu elementu zdejmujemy ze stosu następny do usunięcia, umieszczamy na stosie jego następniki itd...
- jeżeli element drzewa znajduje się w lewej gałęzi to jest mniejszy od swego poprzednika
- jeżeli element drzewa znajduje się w prawej gałęzi to jest większy od swego poprzednika
Oto przykładowe drzewo BST:
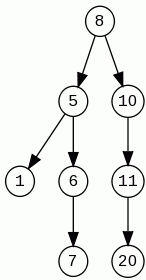
- Wzdłużne - preorder: korzeń, lewe poddrzewo, prawe poddrzewo.
- Poprzeczne - inorder: lewe poddrzewo, korzeń, prawe poddrzewo.
- Wsteczne - postorder: lewe poddrzewo, prawe poddrzewo, korzeń.
Jeśli drzewo BST jest puste (korzeń=nil) należy wstawić element (nie porównujemy go z innymi), w przeciwnym wypadku porównujemy wartość elementu z następnikami każdego węzła (zaczynając od korzenia). Jeżeli wartość elementu jest niewiększa od wartości porównywanego wierzchołka to przechodzimy do lewego następnika, w przeciwnym razie przechodzimy do prawego następnika. Krok ten powtarzamy aż znajdziemy dla naszego elementu odpowiedznie miejsce, tzn. gdy następnik, do którego powinniśmy iść jest pusty (nil). Następnie wstawiamy element jako odpowiedni następnik (prawy, jeśli element jest większy od węzła, lewy jeśli niewiększy).
Usuwanie elementów:
Jeżeli usuwany element nie ma następników to można zwolnić przydzieloną mu pamięć. Jeśli element do usunięcia ma jeden następnik należy go połączyć (następnik) z poprzednikiem usuwanego elementu. Jeśli element ma dwa następniki można go usunąć na dwa sposoby:
- połączyć poprzednik elementu z wierzchołkiem o najmniejszej wartości z prawego poddrzewa usuwanego
- połączyć poprzednik elementu z wierzchołkiem o największej wartości z lewego poddrzewa
Można to zrobić na dwa sposoby: od końca, schodząc za każdym razem od korzenia lub od korzenia. Ta druga metoda jest znacznie szybsza, wymaga jednak zastosowania stosu, na którym umieszczamy następniki usuwanego elementu. Po usunięciu elementu zdejmujemy ze stosu następny do usunięcia, umieszczamy na stosie jego następniki itd...
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Bartosz Bednarczyk | C/C++ | Plik nagłówkowy - C++ | .cpp | .cpp | ***** / 12 |
| Rafał Gawlik | C/C++ | .cpp | .cpp | ***** / 74 | |
| Michał Knasiecki | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 14 |
| Łukasz Guz | Java | .java | .java | ***** / 19 | |
| Marek Rynarzewski | Php | BST + dodatkowe funkcje | .php | .php | ***** / 2 |
Poprawiony: 30 sierpnia 2012 14:38



Cytuję majki90:
Gwoli jasności: następnik = potomek, poprzednik = rodzic, więc zamienne używanie równoważnych określeń nie jest błędem.
Analogicznie w przypadku poprzednika.