Wpisany przez Michał Knasiecki,
28 lipca 2005 23:06
Oto dodatkowe informacje na temat grafów, potrzebne w bardziej skomplikowanych algorytmach.
Kilka definicji:
Stopień wierzchołka - to liczba krawędzi do niego przyległych
Graf regularny - to graf, w którym każdy wierzchołek ma taki sam stopień
Graf planarny - to graf, który można przedstawić na płaszczyźnie tak, by żadne dwie krawędzie się nie przecinały
f-graf - to graf z ograniczonym stopniem wierzchołka, tzn. jego stopień nie może być większy niż f
Graf prosty - to graf bez pętli własnych i krawędzi równoległych
Niezmiennik grafu - to liczba lub ciąg liczb, który zależy tylko od struktury grafu a nie od sposobu jego poetykietowania (np. liczba wierzchołków, liczba krawędzi)
Liczba chromatyczna grafu - to najmniejsza liczba kolorów potrzebnych do pokolorowania wierzchołków grafu tak, by żadne dwa przyległe wierzchołki nie były tego samego koloru
Przykładu do powyższych definicji:
Teraz przejdźmy do bardzo ważnego problemu: generowania grafów losowych.
Istnieje kilka modeli grafów losowych, omówimy najważnejsze:
Kryterium izomorfizmu grafów:
Kilka definicji:
Stopień wierzchołka - to liczba krawędzi do niego przyległych
Graf regularny - to graf, w którym każdy wierzchołek ma taki sam stopień
Graf planarny - to graf, który można przedstawić na płaszczyźnie tak, by żadne dwie krawędzie się nie przecinały
f-graf - to graf z ograniczonym stopniem wierzchołka, tzn. jego stopień nie może być większy niż f
Graf prosty - to graf bez pętli własnych i krawędzi równoległych
Niezmiennik grafu - to liczba lub ciąg liczb, który zależy tylko od struktury grafu a nie od sposobu jego poetykietowania (np. liczba wierzchołków, liczba krawędzi)
Liczba chromatyczna grafu - to najmniejsza liczba kolorów potrzebnych do pokolorowania wierzchołków grafu tak, by żadne dwa przyległe wierzchołki nie były tego samego koloru
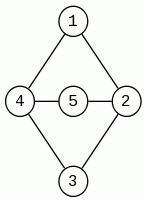
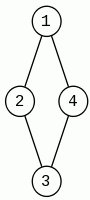
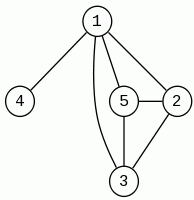
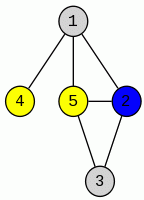
Przykładu do powyższych definicji:
|
|
|
|
Teraz przejdźmy do bardzo ważnego problemu: generowania grafów losowych.
Istnieje kilka modeli grafów losowych, omówimy najważnejsze:
- model G(n,p) - n (liczba wierzchołków) jest dana, p jest tzw. prawdopodobieństwem krawędziowym (0<=p<=1). Liczba p jest określona dla każdej krawędzi, określa ono prawdzopodobieństwo, że dana krawędź znajdzie się w grafie
- model G(n,k) - n jest dana, ze zbioru wszystkich możliwych krawędzi są losowane kolejne krawędzie, lecz tu, w odróżnieniu do poprzedniego modelu, z jednakowym prawdopodobieństwem
- model G(n,f) - n jest dana, f oznacza maksymalny stopień wierzchołka, którego nie można przekroczyć.
- wybór odpowiedniego generatora (zgodnie z powyższymi modelami)
- każdy wygenerowany graf jest weryfikowany, czy spełnia założenia wybranego modelu (np. czy jego największy stopień nie jest większy niż f), grafy które ich nie spełniają są odrzucane, reszta jest zapisywana np. w pliku
- po zakończeniu generowania w pliku znajdują się grafy spełniające założenia danego modelu. Należy jeszcze sprawdzić, czy grafy te są różne, tzn. czy nie ma wśród nich grafów izomorficznych
Kryterium izomorfizmu grafów:
- jednakowa liczba wierzchołków
- jednakowa liczba krawędzi
- jednakowy ciąg stopni wierzchołków
- jendakowe ciągi stopni wierzchołków dla sąsiadów
- jednakowa liczba trójkątów (cykli o długości 3)
- tworzenie macierzy odległości
Poprawiony: 29 sierpnia 2012 21:55


