Wpisany przez Tomasz Lubiński,
25 listopada 2011 19:53
Twórcą algorytmów genetycznych jest John Henry Holland. Nazwa tego rodzaju algorytmów wywodzi się ze sposobu w jaki wyszukiwane jest rozwiązanie. Przypomina ono mieszanie się i dobór genów w trakcie ewolucji.
Rozwiązanie każdego problemu może zostać przedstawione za pomocą pewnego zbioru n parametrów: R = {param1, param2, ..., paramn.
Pewne rozwiązania są lepsze od innych. Zatem każde rozwiązanie ma jakąś wartość, którą będziemy starać się maksymalizować (jeżeli wartość ta oznacza zysk) lub minimalizować (jeżeli wartość ta oznacza koszt).
Niech będzie dana początkowa pula p rozwiązań: R11, R21, ..., Rp1.
Może być ona wynikiem losowania (czyli każde rozwiązanie ma na początku losowe wartości swoich parametrów), bądź wynikiem jakiś różnych przybliżeń dla których spodziewamy się uzyskać zadowalające nas wyniki.
Każda kolejna pula rozwiązań (pokolenie) będzie powstawać poprzez wykonanie następujących kroków:
Postępowanie algorytmu genetycznego możemy więc opisać następującym schematem blokowym:
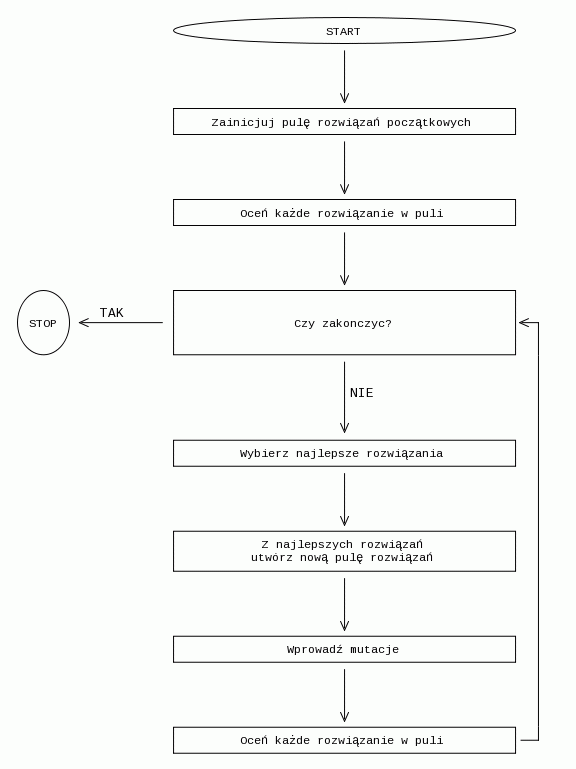
Przyjrzyjmy się teraz kolejnym krokom algorytmu.
Jak z najlepszych rozwiązań tworzyć nowe? Poprzez krzyżowanie. A więc jeżeli nowe rozwiązanie Rnowe będzie tworzone z dwóch innych R1 oraz R2 to krzyżowanie należy przeprowadzić następująco:
Wylosuj liczbę od 0 do 1, jeżeli wylosowana liczba jest mniejsza od 0.5 to do Rnowe weź param1 z R1 w przeciwnym wypadku weź go z R2.
Wylosuj liczbę od 0 do 1, jeżeli wylosowana liczba jest mniejsza od 0.5 to do Rnowe param2 z R1 w przeciwnym wypadku weź go z R2.
...
Wylosuj liczbę od 0 do 1, jeżeli wylosowana liczba jest mniejsza od 0.5 to do Rnowe paramn z R1 w przeciwnym wypadku weź go z R2.
Podobnie można wyobrazić sobie krzyżowanie, w którym bierze większa liczba osobników.
Jak wprowadzać mutacje? W zależności od wielkości mutacji wybieramy losowo 1, 2, ... lub n parametrów i zmieniamy je o losową wartość. Wielkość tej zmiany również zależy od wielkości mutacji.
Jak wybrać rozwiązania, które utworzą nowe pokolenie? Istnieje kilka sposobów.
Rozwiązanie każdego problemu może zostać przedstawione za pomocą pewnego zbioru n parametrów: R = {param1, param2, ..., paramn.
Pewne rozwiązania są lepsze od innych. Zatem każde rozwiązanie ma jakąś wartość, którą będziemy starać się maksymalizować (jeżeli wartość ta oznacza zysk) lub minimalizować (jeżeli wartość ta oznacza koszt).
Niech będzie dana początkowa pula p rozwiązań: R11, R21, ..., Rp1.
Może być ona wynikiem losowania (czyli każde rozwiązanie ma na początku losowe wartości swoich parametrów), bądź wynikiem jakiś różnych przybliżeń dla których spodziewamy się uzyskać zadowalające nas wyniki.
Każda kolejna pula rozwiązań (pokolenie) będzie powstawać poprzez wykonanie następujących kroków:
- oceń każde rozwiązanie w puli (pokoleniu)
- wybierz najlepsze rozwiązania (osobniki) i na ich podstawie wygeneruj nową pulę (pokolenie)
- wprowadź mutacje
Postępowanie algorytmu genetycznego możemy więc opisać następującym schematem blokowym:

Przyjrzyjmy się teraz kolejnym krokom algorytmu.
Jak z najlepszych rozwiązań tworzyć nowe? Poprzez krzyżowanie. A więc jeżeli nowe rozwiązanie Rnowe będzie tworzone z dwóch innych R1 oraz R2 to krzyżowanie należy przeprowadzić następująco:
Wylosuj liczbę od 0 do 1, jeżeli wylosowana liczba jest mniejsza od 0.5 to do Rnowe weź param1 z R1 w przeciwnym wypadku weź go z R2.
Wylosuj liczbę od 0 do 1, jeżeli wylosowana liczba jest mniejsza od 0.5 to do Rnowe param2 z R1 w przeciwnym wypadku weź go z R2.
...
Wylosuj liczbę od 0 do 1, jeżeli wylosowana liczba jest mniejsza od 0.5 to do Rnowe paramn z R1 w przeciwnym wypadku weź go z R2.
Podobnie można wyobrazić sobie krzyżowanie, w którym bierze większa liczba osobników.
Jak wprowadzać mutacje? W zależności od wielkości mutacji wybieramy losowo 1, 2, ... lub n parametrów i zmieniamy je o losową wartość. Wielkość tej zmiany również zależy od wielkości mutacji.
Jak wybrać rozwiązania, które utworzą nowe pokolenie? Istnieje kilka sposobów.
- Rozwiązania, które użyjemy do utworzenia nowego wybieramy spośród całej populacji, przy czym prawdopodobieństwo wybrania rozwiązań (osobników) lepszych jest proporcjonalnie większe od prawdopodobieństwa wybrania osobników gorszych.
- Spośród rozwiązań wybieramy e (e < p) najlepszych rozwiązań, które tworzą tzw. elitę i reprodukcję wykonujemy używając tylko nich
Poprawiony: 25 listopada 2011 19:56


