Wpisany przez Tomasz Lubiński,
17 maja 2007 21:52
Algorytm Bresenhama (algorytm z punktem środkowym) służy do efektywnego kreślenia dwuwymiarowych krzywych na ekranie komputera. Proces taki nazywamy rasteryzacją, ponieważ idealna krzywa nie przechodzi dokładnie przez środek pikseli, które zapalamy. Włączamy te piksle, które znajdują się najbliżej takiej idealnej krzywej. Algorytm Bresenhama możemy stosować dla krzywych, które spełniają poniższe warunki:
Jeżeli krzywa nie spełnia tych warunków, to kreśli się ją za pomocą fragmentów, które je spełniają. Dodatkowo też wykorzystuje się symetrię.
Metoda wymaga by krzywą opisywała funkcja uwikłana postaci f(x, y) = 0 np. dla funkcji opisującej okrąg wartość 0 oznacza punkt okręu, wartość większa od 0 oznacza punkt na zewnątrz okręgu a wartość mniejsza od 0 oznacza punkt wewnątrz okręgu.
Załóżmy, że krzywa w przedziale < xp, xk > spełnia powyższe założenia. Algorytm Bresenhama zaczynie więc swoje działanie od punktu (xp, yp). Zapalany jest zatem piksel o tych współrzędnych. Następnie współrzędna x jest zwiększana o 1, czyli kolejny piksel ma współrzędną x = xp + 1. Teraz pozostaje wyznaczyć współrzędną y. Dzięki pierwszemu warunkowi (nachylenie krzywej) wybór ten ogranicza się na piksele zaznaczone na rysunku poprzez A i B. Sprawdzamy zatem punkt przecięcia krzywej z linią pionową xp + 1. Jeśli punkt ten jest bliżej punktu A to wybierany jest ten właśnie punkt, w przeciwnym razie wybieramy punkt B. Na rysunku poniżej przedstawioną mamy sytuację, w której zapalilibyśmy piksel A.
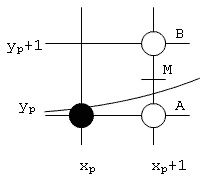
Do szybkiego stwierdzenia czy przecięcie jest pod punktem środkowym wykorzystamy, wspomnianą już, cechę funkcji uwikłanej. Załóżmy, że f(x, y) > 0 dla punktów powyżej krzywej. Jeżeli więc wartość funkcji w punkcie środkowym f(xp + 1, yp + 0.5) jest mniejsza od zera, to wybrany zostanie punkt A, w przeciwnym razie punkt B.
Ponieważ współrzędne x i y zmieniają się o stałe kroki, tak więc wartość funkcji w punkcie przecięcia z osią pionową można przewidzieć. Wartość tą oznaczymy przez d i nazywać będziemy zmienną decyzyjną - od jej wartości zależeć będzie czy idziemy w kierunku E czy NE. Wartość zmiennej decyzyjnej d wynosi:
Tak więc przy wyborze punktu A wartość funkcji zmieni się o dA - dp, po wybraniu punku B o dB - dp. Różnice te są nazywane różnicami pierwszego rzędu. Jeśli nie są stałe, a więc zależą od współrzędnych, to można policzyć odpowiednie przyrosty również dla nich — te przyrosty nazywają się różnicami drugiego rzędu.
Algorytm w pseudokodzie możemy zatem zapisać następująco:
Przykłady zastosowania algorytmu Bresenhama odnajdziemy w:
- kąt między styczną rysowanej krzywej a osią OX musi mieścić się w zakresie od 0 do 45 stopni włącznie, zatem jeżeli krzywa opisana jest wzorem postaci y = f(x) to musi ona spełniać warunek 0 ≤ f '(x) ≤ 1
- krzywa musi być monotoniczna: nierosnąca, albo niemalejąca
Jeżeli krzywa nie spełnia tych warunków, to kreśli się ją za pomocą fragmentów, które je spełniają. Dodatkowo też wykorzystuje się symetrię.
Metoda wymaga by krzywą opisywała funkcja uwikłana postaci f(x, y) = 0 np. dla funkcji opisującej okrąg wartość 0 oznacza punkt okręu, wartość większa od 0 oznacza punkt na zewnątrz okręgu a wartość mniejsza od 0 oznacza punkt wewnątrz okręgu.
Załóżmy, że krzywa w przedziale < xp, xk > spełnia powyższe założenia. Algorytm Bresenhama zaczynie więc swoje działanie od punktu (xp, yp). Zapalany jest zatem piksel o tych współrzędnych. Następnie współrzędna x jest zwiększana o 1, czyli kolejny piksel ma współrzędną x = xp + 1. Teraz pozostaje wyznaczyć współrzędną y. Dzięki pierwszemu warunkowi (nachylenie krzywej) wybór ten ogranicza się na piksele zaznaczone na rysunku poprzez A i B. Sprawdzamy zatem punkt przecięcia krzywej z linią pionową xp + 1. Jeśli punkt ten jest bliżej punktu A to wybierany jest ten właśnie punkt, w przeciwnym razie wybieramy punkt B. Na rysunku poniżej przedstawioną mamy sytuację, w której zapalilibyśmy piksel A.

Do szybkiego stwierdzenia czy przecięcie jest pod punktem środkowym wykorzystamy, wspomnianą już, cechę funkcji uwikłanej. Załóżmy, że f(x, y) > 0 dla punktów powyżej krzywej. Jeżeli więc wartość funkcji w punkcie środkowym f(xp + 1, yp + 0.5) jest mniejsza od zera, to wybrany zostanie punkt A, w przeciwnym razie punkt B.
Ponieważ współrzędne x i y zmieniają się o stałe kroki, tak więc wartość funkcji w punkcie przecięcia z osią pionową można przewidzieć. Wartość tą oznaczymy przez d i nazywać będziemy zmienną decyzyjną - od jej wartości zależeć będzie czy idziemy w kierunku E czy NE. Wartość zmiennej decyzyjnej d wynosi:
- w punkcie (xp, yp): dp = f(xp + 1, yp + 0.5)
- w punkcie A: dA = f(xp + 2, yp + 0.5)
- natomiast w punkcie B: dB = f(xp + 2, yp + 1.5)
Tak więc przy wyborze punktu A wartość funkcji zmieni się o dA - dp, po wybraniu punku B o dB - dp. Różnice te są nazywane różnicami pierwszego rzędu. Jeśli nie są stałe, a więc zależą od współrzędnych, to można policzyć odpowiednie przyrosty również dla nich — te przyrosty nazywają się różnicami drugiego rzędu.
Algorytm w pseudokodzie możemy zatem zapisać następująco:
y = yp
d = f(x+1, y+0.5)
while x < xk
putpixel(x, y)
if d < 0 //idziemy w kierunku NE
d = d+f(x+2, y+1.5)-f(x+1, y+0.5)
y = y+1
x = x+1
else //idziemy w kierunku E
d = d+f(x+2, y+0.5)-f(x+1, y+0.5)
x = x+1
Algorytm może działać zarówno na liczbach zmiennoprzecinkowych jak i całkowitych, ale ze względów wydajnościowych wykorzystuje się najczęściej realizacje całkowitoliczbowe. Zatem jeżeli początkowa wartość zmiennej decyzyjnej d lub jej przyrosty wychodzą nam ułamkowe, to mnożymy zarówno zmienną decyzyjną d jak i jej przyrosty tak by uzyskać liczby całkowite. Możemy tak zrobić gdyż do decyzji bierzemy pod uwagę jedynie znak zmiennej decyzyjnej d.Przykłady zastosowania algorytmu Bresenhama odnajdziemy w:
- algorytmie rasteryzacji odcinka,
- algorytmie rasteryzacji okręgu - tutaj kreślimy wyłącznie wycinek okręgu spełniający założenia algorytmu Bresenhama a resztę uzykujemy poprzez zastosowanie symetrii,
- algorytmie rasteryzacji elipsy - tutaj kreślimy odrębnie dwa wycinki elpisy spełniające założenia algorytmu Bresenhama a resztę uzykujemy poprzez zastosowanie symetrii.
Poprawiony: 20 czerwca 2011 21:37



A na poważnie, to tak zapytam, matematyka w szkole była? Bo jeżeli ni, to nie spiesz się z programowaniem, zdążysz.