Wpisany przez Tomasz Lubiński,
15 maja 2007 19:05
W trakcie kreślenia elipsy wykorzystamy jej czterokrotną symetrię. Najpierw zajmiemy się obliczeniami niezbędnymi do narysowania pierwszego wycinka zaznaczonego na rysunku poniżej kolorem niebieskim. Korzystając ze wspomnianej czterokrotnej symetrii wykreślimy część elipsy
oznaczoną linią ciągłą.
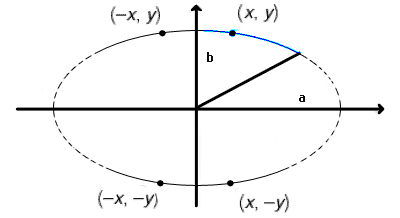
Równanie elipsy o środku we współrzędnych (0, 0) i promieniach a oraz b to: F(x, y) = b2x2 + a2y2 - a2b2
Dla punktów leżących na elipsie F(x, y) = 0
Dla punktów leżących na zewnątrz elipsy F(x, y) > 0
Dla punktów leżących wewnątrz elipsy F(x, y) < 0
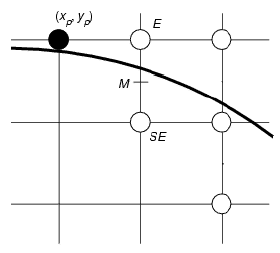 Jak widać na rysunku po prawej, idealna elipsa nie przechodzi dokładnie przez punkty, które zapalamy. Należy więc wybrać punkty leżące najbliżej idealnej elipsy. Na czarno zaznaczony mamy aktualny punkt (xp, yp). Jak już powiedzieliśmy wcześniej rysować będziemy tylko początkowy wycinek elipsy. W takim wypadku zawsze będziemy musieli podjąć decyzję czy zapalić punkt E (położony na wschód), czy punkt SE (położony na południowy wschód). Który z tych dwóch punktów wybrać? Oczywiście ten leżący bliżej idealnej elipsy. Na rysunku wprowadzono punkt M, leżący dokładnie pośrodku punktów E oraz SE. Zatem jeżeli elipsa przecina się nad punktem M to wybieramy E, jeżeli pod lub dokładnie w wybieramy SE. By efektywnie podejmować taką decyzję wprowadzimy zmienną decyzyjną d = F(xp + 1, yp - 0.5) = b2(xp+1)2 + a2(yp-0.5)2 - a2b2
Jak widać na rysunku po prawej, idealna elipsa nie przechodzi dokładnie przez punkty, które zapalamy. Należy więc wybrać punkty leżące najbliżej idealnej elipsy. Na czarno zaznaczony mamy aktualny punkt (xp, yp). Jak już powiedzieliśmy wcześniej rysować będziemy tylko początkowy wycinek elipsy. W takim wypadku zawsze będziemy musieli podjąć decyzję czy zapalić punkt E (położony na wschód), czy punkt SE (położony na południowy wschód). Który z tych dwóch punktów wybrać? Oczywiście ten leżący bliżej idealnej elipsy. Na rysunku wprowadzono punkt M, leżący dokładnie pośrodku punktów E oraz SE. Zatem jeżeli elipsa przecina się nad punktem M to wybieramy E, jeżeli pod lub dokładnie w wybieramy SE. By efektywnie podejmować taką decyzję wprowadzimy zmienną decyzyjną d = F(xp + 1, yp - 0.5) = b2(xp+1)2 + a2(yp-0.5)2 - a2b2
Jeżeli d ≥ 0 to wybieramy kierunek SE.
Jeżeli d < 0 to wybieramy kierunek E.
Początkowa wartość zmiennej decyzyjnej d wynosić będzie F(x0 + 1, y0 - 0.5), gdzie (x0, y0) jest pierwszym rysowanym punktem elipsy - pierwszy rysujemy punkt na samym szczycie elipsy zatem (x0, y0) = (0, b), podstawiając to do przedstawionego wzoru otrzymujemy:
F(0 + 1, b - 0.5) = b2 + a2(b-0.5)2 - a2b2 = b2 + a2b2 + a2b + 0.25a2 - a2b2 = b2 - a2b + 0.25a2
W zależności od wybranego ruchu (SE lub E) inaczej zmieniać będziemy aktualną wartość zmiennej decyzyjnej d
Ponieważ początkowa wartość zmiennej decyzyjnej d wyszła nam ułamkowa, a nam zależy na jak najszybszych obliczeniach, zamienimy ją na liczbę całkowitą (operacje na liczbach stałoprzecinkowych wykonywane są szybciej niż na liczbach zmiennoprzecinkowych). Przemnożymy zatem jej wartości przez 4 (decyzja zależy wyłącznie od znaku zmiennej decyzyjnej, dlatego możemy tak postąpić). I tak ostatecznie otrzymujemy:
Obliczenia te należy prowadzić tak długo, aż osiągniemy punkt w którym nachylenie przekracza -1. Do obliczenia tego punktu wykorzystuje się pochodną funkcji jednej zmiennej. Punkt ten to:
x2 = a4 / (a2 + b2). W ten sposób wykreślimy część elipsy zaznaczoną linią ciągłą.
Teraz zajmiemy się wykreśleniem części elipsy zaznaczonej linią przerywaną. Zwróćmy uwagę, że jeżeli zamienimy w kreślonej przez nas elipsie półosie a z b wówczas opisanym przez nas algorytmem wykreślimy część oznaczoną na rysunku poniżej kolorem zielonym.
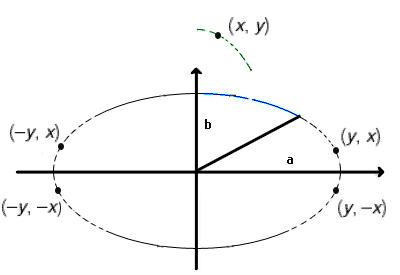
Jeżeli natomiast zamienimy teraz współrzędne x z y i potraktujemy je wspomnianą na początku czterokrotną symetrią to otrzymamy część elipsy zaznaczoną linią przerywaną.
Wyznaczymy pierwsze 4 punkty elipsy o środku we współrzędnych (0, 0) i a=10 oraz b=15.
Pierwszy punkt to (0, b) = (0, 15)
Początkowa wartość zmiennej decyzyjnej to d = 4b2 - 4a2b + a2 = 4*255 - 4*15*100 + 100 = 900 - 6000 + 100 = -5000
Jej wartość jest mniejsza niż zero, a więc wybieramy kierunek E.
Zatem kolejny punkt to (0 + 1, 15) = (1, 15)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = d + 8b2x + 12b2 = -5000 + 0 + 2700 = -2300
Jej wartość nadal jest mniejsza niż zero, a więc wybieramy kierunek E.
Zatem kolejny punkt to (1 + 1, 15) = (2, 15)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = d + 8b2x + 12b2 = -2300 + 1800 + 2700 = 2200
Jej wartość jest większa niż zero, więc wybieramy kierunek SE.
Zatem kolejny punkt to (2 + 1, 15 + 1) = (3, 16)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = d + 8b2x + 12b2 - 8a2y + 8a2 = 2200 + 3600 + 2700 - 12000 + 800 = -2700
Obliczenia te należy kontynuować dopóki x2 < a4 / (a2 + b2), pamiętać też należy, że każdy obliczony punkt "potraktować" trzeba wspomnianą już czterokrotną symetrią. W ten sposób powstanie część elipsy oznaczona linią ciągłą. Część oznaczoną linią przerywaną obliczymy zamieniając a z b
A więc a=15 oraz b=10.
Pierwszy punkt to (0, b) = (0, 10)
Początkowa wartość zmiennej decyzyjnej to d = 4b2 - 4a2b + a2 = 400 - 9000 + 225 = -8375
Jej wartość jest mniejsza niż zero, a więc wybieramy kierunek E.
Zatem kolejny punkt to (0 + 1, 10) = (1, 10)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = d + 8b2x + 12b2 = -8375 + 0 + 1200 = -7175
Jej wartość nadal jest mniejsza niż zero, a więc wybieramy kierunek E.
Zatem kolejny punkt to (1 + 1, 10) = (2, 10)
Obliczenia te należy kontynuować dopóki x2 < a4 / (a2 + b2), pamiętać też należy, że każdy obliczony punkt "potraktować" trzeba wspomnianą już czterokrotną symetrią, przed którą jednak należy zamienić x z y. Zatem zapalamy teraz punkty (0, 10) "potraktowany" czterokrotną symetrią i zamienione x z y czyli (10, 0), (10, -0), (-10, 0), (-10, -0), i tak dalej z kolejnymi punktami
Gdyby elipsa, którą chcemy kreślić miała środek w punkcie innym niż (0, 0), obliczenia przebiegałyby identycznie jak dla elipsy o współrzędnych środka (0, 0) tylko do ostatecznych punktów, które rysowalibyśmy dodalibyśmy przesunięcie równe środkowi. Tzn. dla elipsy, dla której a=10 oraz b=15 i środku we współrzędnych (15, 30) otrzymalibyśmy identyczne obliczenia jak poprzednio tylko punkty, które narysowalibyśmy byłyby następujące:
(0 + 15, 15 + 30) = (15, 45)
(1 + 15, 15 + 30) = (16, 45)
(2 + 15, 15 + 30) = (17, 45)
(3 + 15, 16 + 30) = (18, 46)
...
(10 + 15, 0 + 30) = (45, 30)
...

Równanie elipsy o środku we współrzędnych (0, 0) i promieniach a oraz b to: F(x, y) = b2x2 + a2y2 - a2b2
Dla punktów leżących na elipsie F(x, y) = 0
Dla punktów leżących na zewnątrz elipsy F(x, y) > 0
Dla punktów leżących wewnątrz elipsy F(x, y) < 0
 Jak widać na rysunku po prawej, idealna elipsa nie przechodzi dokładnie przez punkty, które zapalamy. Należy więc wybrać punkty leżące najbliżej idealnej elipsy. Na czarno zaznaczony mamy aktualny punkt (xp, yp). Jak już powiedzieliśmy wcześniej rysować będziemy tylko początkowy wycinek elipsy. W takim wypadku zawsze będziemy musieli podjąć decyzję czy zapalić punkt E (położony na wschód), czy punkt SE (położony na południowy wschód). Który z tych dwóch punktów wybrać? Oczywiście ten leżący bliżej idealnej elipsy. Na rysunku wprowadzono punkt M, leżący dokładnie pośrodku punktów E oraz SE. Zatem jeżeli elipsa przecina się nad punktem M to wybieramy E, jeżeli pod lub dokładnie w wybieramy SE. By efektywnie podejmować taką decyzję wprowadzimy zmienną decyzyjną d = F(xp + 1, yp - 0.5) = b2(xp+1)2 + a2(yp-0.5)2 - a2b2
Jak widać na rysunku po prawej, idealna elipsa nie przechodzi dokładnie przez punkty, które zapalamy. Należy więc wybrać punkty leżące najbliżej idealnej elipsy. Na czarno zaznaczony mamy aktualny punkt (xp, yp). Jak już powiedzieliśmy wcześniej rysować będziemy tylko początkowy wycinek elipsy. W takim wypadku zawsze będziemy musieli podjąć decyzję czy zapalić punkt E (położony na wschód), czy punkt SE (położony na południowy wschód). Który z tych dwóch punktów wybrać? Oczywiście ten leżący bliżej idealnej elipsy. Na rysunku wprowadzono punkt M, leżący dokładnie pośrodku punktów E oraz SE. Zatem jeżeli elipsa przecina się nad punktem M to wybieramy E, jeżeli pod lub dokładnie w wybieramy SE. By efektywnie podejmować taką decyzję wprowadzimy zmienną decyzyjną d = F(xp + 1, yp - 0.5) = b2(xp+1)2 + a2(yp-0.5)2 - a2b2Jeżeli d ≥ 0 to wybieramy kierunek SE.
Jeżeli d < 0 to wybieramy kierunek E.
Początkowa wartość zmiennej decyzyjnej d wynosić będzie F(x0 + 1, y0 - 0.5), gdzie (x0, y0) jest pierwszym rysowanym punktem elipsy - pierwszy rysujemy punkt na samym szczycie elipsy zatem (x0, y0) = (0, b), podstawiając to do przedstawionego wzoru otrzymujemy:
F(0 + 1, b - 0.5) = b2 + a2(b-0.5)2 - a2b2 = b2 + a2b2 + a2b + 0.25a2 - a2b2 = b2 - a2b + 0.25a2
W zależności od wybranego ruchu (SE lub E) inaczej zmieniać będziemy aktualną wartość zmiennej decyzyjnej d
- jeżeli wybrano kierunek E, to zwiększamy jedynie x:
dold = F(xp + 1, yp - 0.5) = b2(xp+1)2 + a2(yp-0.5)2 - a2b2
dnew = F(xp + 2, yp - 0.5) = b2(xp+2)2 + a2(yp-0.5)2 - a2b2 = b2xp2 + b24xp + b24 + a2(yp-0.5)2 - a2b2 = dold + b22xp + b23 - jeżeli wybrano kierunek SE, to zwiększamy x i zmniejszamy y:
dold = F(xp + 1, yp - 0.5) = b2(xp+1)2 + a2(yp-0.5)2 - a2b2
dnew = F(xp + 2, yp - 1.5) = b2xp2 + b24xp + b24 + a2yp2 - a23yp + a22.25 = dold + b22xp + b23 - 2a2yp + a22
Ponieważ początkowa wartość zmiennej decyzyjnej d wyszła nam ułamkowa, a nam zależy na jak najszybszych obliczeniach, zamienimy ją na liczbę całkowitą (operacje na liczbach stałoprzecinkowych wykonywane są szybciej niż na liczbach zmiennoprzecinkowych). Przemnożymy zatem jej wartości przez 4 (decyzja zależy wyłącznie od znaku zmiennej decyzyjnej, dlatego możemy tak postąpić). I tak ostatecznie otrzymujemy:
- wartość początkowa: d = 4b2 - 4a2b + a2
- inkrementacja przy wyborze kierunku E: d = d + 8b2x + 12b2
- inkrementacja przy wyborze kierunku SE: d = d + 8b2x + 12b2 - 8a2y + 8a2
Obliczenia te należy prowadzić tak długo, aż osiągniemy punkt w którym nachylenie przekracza -1. Do obliczenia tego punktu wykorzystuje się pochodną funkcji jednej zmiennej. Punkt ten to:
x2 = a4 / (a2 + b2). W ten sposób wykreślimy część elipsy zaznaczoną linią ciągłą.
Teraz zajmiemy się wykreśleniem części elipsy zaznaczonej linią przerywaną. Zwróćmy uwagę, że jeżeli zamienimy w kreślonej przez nas elipsie półosie a z b wówczas opisanym przez nas algorytmem wykreślimy część oznaczoną na rysunku poniżej kolorem zielonym.

Jeżeli natomiast zamienimy teraz współrzędne x z y i potraktujemy je wspomnianą na początku czterokrotną symetrią to otrzymamy część elipsy zaznaczoną linią przerywaną.
Przykład:
Wyznaczymy pierwsze 4 punkty elipsy o środku we współrzędnych (0, 0) i a=10 oraz b=15.
Pierwszy punkt to (0, b) = (0, 15)
Początkowa wartość zmiennej decyzyjnej to d = 4b2 - 4a2b + a2 = 4*255 - 4*15*100 + 100 = 900 - 6000 + 100 = -5000
Jej wartość jest mniejsza niż zero, a więc wybieramy kierunek E.
Zatem kolejny punkt to (0 + 1, 15) = (1, 15)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = d + 8b2x + 12b2 = -5000 + 0 + 2700 = -2300
Jej wartość nadal jest mniejsza niż zero, a więc wybieramy kierunek E.
Zatem kolejny punkt to (1 + 1, 15) = (2, 15)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = d + 8b2x + 12b2 = -2300 + 1800 + 2700 = 2200
Jej wartość jest większa niż zero, więc wybieramy kierunek SE.
Zatem kolejny punkt to (2 + 1, 15 + 1) = (3, 16)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = d + 8b2x + 12b2 - 8a2y + 8a2 = 2200 + 3600 + 2700 - 12000 + 800 = -2700
Obliczenia te należy kontynuować dopóki x2 < a4 / (a2 + b2), pamiętać też należy, że każdy obliczony punkt "potraktować" trzeba wspomnianą już czterokrotną symetrią. W ten sposób powstanie część elipsy oznaczona linią ciągłą. Część oznaczoną linią przerywaną obliczymy zamieniając a z b
A więc a=15 oraz b=10.
Pierwszy punkt to (0, b) = (0, 10)
Początkowa wartość zmiennej decyzyjnej to d = 4b2 - 4a2b + a2 = 400 - 9000 + 225 = -8375
Jej wartość jest mniejsza niż zero, a więc wybieramy kierunek E.
Zatem kolejny punkt to (0 + 1, 10) = (1, 10)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = d + 8b2x + 12b2 = -8375 + 0 + 1200 = -7175
Jej wartość nadal jest mniejsza niż zero, a więc wybieramy kierunek E.
Zatem kolejny punkt to (1 + 1, 10) = (2, 10)
Obliczenia te należy kontynuować dopóki x2 < a4 / (a2 + b2), pamiętać też należy, że każdy obliczony punkt "potraktować" trzeba wspomnianą już czterokrotną symetrią, przed którą jednak należy zamienić x z y. Zatem zapalamy teraz punkty (0, 10) "potraktowany" czterokrotną symetrią i zamienione x z y czyli (10, 0), (10, -0), (-10, 0), (-10, -0), i tak dalej z kolejnymi punktami
Gdyby elipsa, którą chcemy kreślić miała środek w punkcie innym niż (0, 0), obliczenia przebiegałyby identycznie jak dla elipsy o współrzędnych środka (0, 0) tylko do ostatecznych punktów, które rysowalibyśmy dodalibyśmy przesunięcie równe środkowi. Tzn. dla elipsy, dla której a=10 oraz b=15 i środku we współrzędnych (15, 30) otrzymalibyśmy identyczne obliczenia jak poprzednio tylko punkty, które narysowalibyśmy byłyby następujące:
(0 + 15, 15 + 30) = (15, 45)
(1 + 15, 15 + 30) = (16, 45)
(2 + 15, 15 + 30) = (17, 45)
(3 + 15, 16 + 30) = (18, 46)
...
(10 + 15, 0 + 30) = (45, 30)
...
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Andrzej Borucki | C# | MS Visual Studio 2010 | .cs | .cs | ***** / 2 |
| Tomasz Lubiński | C/C++ | Borland Builder 6 | .cpp | .cpp | ***** / 4 |
| Andrzej Borucki | C/C++ | Qt Creator | .cpp | .cpp | ***** / 0 |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 1 |
Poprawiony: 01 września 2012 14:06


