Wpisany przez Michał Knasiecki,
01 sierpnia 2005 01:07
Jednym z podstawowych elementów wykorzystywanych w grafice (obok punktu) jest odcinek. Każda scena składa się z brył, każda z brył zbudowana jest z tzw. prymitywów a każdy prymityw składa się z odcinków. Aby efektywnie przetwarzać grafikę (np. wyświetlać animacje, gry itp...) należy maksymalnie skrócić czas wyświetlania każdej klatki, a co za tym idzie stosować obliczeniowo najtańsze algorytmy wyświetlania. Zajmiemy się obecnie algorytmem wyświetlania odcinka.
Aby wykreślić odcinek musimy mieć dane dwa punkty: A=(xA, yA) i B=(xB, yB). Za ich pomocą będziemy obliczać współrzędne pozostałych punktów odcinka. Należy przy tym pamiętać, że odcinek w komputerze nie składa się z nieskończenie wielu punktów, wynika to z faktu, że każdy punkt monitora ma współrzędne o wartości całkowitej. dzięki temu możemy z góry wyznaczyć rzędne wszystkich punktów odcinka, dla xB>xA rzędne te mają wartości: xA, xA+1, xA+2...xB. Znając te wartości możemy obliczyć łatwo odcięte tych punktów korzystając z równania kierunkowego prostej. To samo można jednak uzyskać szybciej stosując opisany poniżej algorytm z punktem środkowym.
Zwróćmy uwagę na kilka szczegółów:
Przeanalizujmy rysunek poniżej:
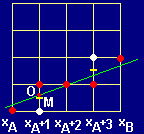
Zaznaczono na nim zielonym kolorem prostą przechodzącą przez punkty A i B (o rzędnych odpowiednio xA i xB) Kolorem czerwonym zaznaczono kolejne punkty (piksele) zapalenie których spowoduje wyświetlenie odcinka zbliżonego wyglądem do tego idealnego. Zajmijmy się punktem o rzędnej xA+1. Jak widać na rysunku, punkt odcinka idealnego o tej rzędnej (punkt O) nie ma odciętej o wartości całkowitej. Należy więc wybrać punkt leżący najbliżej punktu O mający całkowitą odciętą. Do wyboru mamy tylko dwa takie punkty: leżący bezpośrednio nad odcinkiem idealnym (zaznaczony na czerwono) oraz punkt leżący pod nim (biały). Dodatkowo, żółtą kreską zaznaczono punkt M, leżący dokładnie pomiędzy tymi punktami. Który z tych dwóch punktów wybrać? Oczywiście ten leżący bliżej punktu O, a ściślej mówiąc:
Jeżeli d>0 wybieramy punkt nad odcinkiem idealnym, w przeciwnym wypadku wybieramy punkt leżący pod nim.
Kolejne wartości d obliczamy w sposób przyrostowy:
Aby zapewnić działania wyłącznie na liczbach całkowitych (patrz d0) zmienia się wartość funkcji f mnożąc ją przez 2 (dzięki czemu likwiduje się ułamek 0.5d, choć znak funkcji pozostaje niezmieniony)
Aby wykreślić odcinek musimy mieć dane dwa punkty: A=(xA, yA) i B=(xB, yB). Za ich pomocą będziemy obliczać współrzędne pozostałych punktów odcinka. Należy przy tym pamiętać, że odcinek w komputerze nie składa się z nieskończenie wielu punktów, wynika to z faktu, że każdy punkt monitora ma współrzędne o wartości całkowitej. dzięki temu możemy z góry wyznaczyć rzędne wszystkich punktów odcinka, dla xB>xA rzędne te mają wartości: xA, xA+1, xA+2...xB. Znając te wartości możemy obliczyć łatwo odcięte tych punktów korzystając z równania kierunkowego prostej. To samo można jednak uzyskać szybciej stosując opisany poniżej algorytm z punktem środkowym.
Zwróćmy uwagę na kilka szczegółów:
Przeanalizujmy rysunek poniżej:

Zaznaczono na nim zielonym kolorem prostą przechodzącą przez punkty A i B (o rzędnych odpowiednio xA i xB) Kolorem czerwonym zaznaczono kolejne punkty (piksele) zapalenie których spowoduje wyświetlenie odcinka zbliżonego wyglądem do tego idealnego. Zajmijmy się punktem o rzędnej xA+1. Jak widać na rysunku, punkt odcinka idealnego o tej rzędnej (punkt O) nie ma odciętej o wartości całkowitej. Należy więc wybrać punkt leżący najbliżej punktu O mający całkowitą odciętą. Do wyboru mamy tylko dwa takie punkty: leżący bezpośrednio nad odcinkiem idealnym (zaznaczony na czerwono) oraz punkt leżący pod nim (biały). Dodatkowo, żółtą kreską zaznaczono punkt M, leżący dokładnie pomiędzy tymi punktami. Który z tych dwóch punktów wybrać? Oczywiście ten leżący bliżej punktu O, a ściślej mówiąc:
- jeżeli punkt O leży nad punktem M, wybieramy punkt nad odcinkiem (ten czerwony)
- w przeciwnym razie wybieramy punkt pod odcinkiem (biały)
f(x,y)=ax+by+c
Jest to funkcja opisująca prostą. Wprowadzamy dwie dodatkowe zmienne pomocnicze:
dy = y_B - y_A\\
dx = x_B - x_A
za ich pomocą możemy otrzymać równanie prostej przechodzącej przez punktu A i B:
y = \frac{dy}{dx}x + B
Używając nowych zmiennych nasza funkcja ma postać:
f(x,y)=dy*x-dx*y+B*dx
Dla dowolnego punktu P=(x,y) mamy:
- jeżeli f(x,y)=0 - punkt P leży na odcinku
- jeżeli f(x,y)>0 - punkt P leży pod odcinkiem
- jeżeli f(x,y)<0 - punkt P leży nad odcinkiem
d = f(M) = f(x_k+1, y_k+0.5) = a(x_k+1) + b(y_k+0.5) + c
gdzie (xk, yk) jest punktem poprzedzającym obliczany punkt. Jeżeli d>0 wybieramy punkt nad odcinkiem idealnym, w przeciwnym wypadku wybieramy punkt leżący pod nim.
Kolejne wartości d obliczamy w sposób przyrostowy:
- jeżeli wybrano punkt pod odcinkiem, wówczas d' = d + a
- w przeciwnym wypadku d' = d+a +b
Aby zapewnić działania wyłącznie na liczbach całkowitych (patrz d0) zmienia się wartość funkcji f mnożąc ją przez 2 (dzięki czemu likwiduje się ułamek 0.5d, choć znak funkcji pozostaje niezmieniony)
f(x,y) = 2(ax + by + c)
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Andrzej Borucki | C# | MS Visual Studio 2010 | .cs | .cs | ***** / 2 |
| Andrzej Borucki | C/C++ | Qt Creator | .cpp | .cpp | ***** / 1 |
Poprawiony: 01 września 2012 14:04


