W trakcie kreślenia okręgu wykorzystamy jego ośmiokrtoną symetrię. Do pełnego narysowania okręgu wystarczy wykonać obliczenia tylko dla wycinka od 0 do 45 stopni (czyli dla punktów dla których spełniony jest warunek y > x). Pozostałe fragmenty mogą być wyświetlone symetrycznie tak jak przedstawiono to na schemacie poniżej:
Równanie okręgu o środku we współrzędnych (0, 0) i promieniu R to: F(x, y) = x² + y² - R²
Dla punktów leżących na okręgu F(x, y) = 0
Dla punktów leżących na zewnątrz okręgu F(x, y) > 0
Dla punktów leżących wewnątrz okręgu F(x, y) < 0

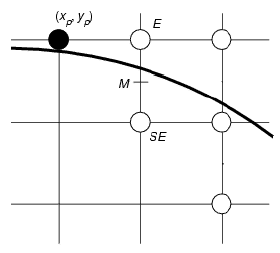Jak widać na rysunku po prawej, idealny okrąg nie przechodzi dokładnie przez punkty, które zapalamy. Należy więc wybrać punkty leżące najbliżej idealnego okręgu. Na czarno zaznaczony mamy aktualny punkt (x_p, y_p). Jak już powiedzieliśmy wcześniej rysować będziemy tylko początkowe 45 stopni okręgu. W takim wypadku zawsze będziemy musieli podjąc decyzję czy zapalić punkt E (położony na wschód), czy punkt SE (położony na południowy wschód). Który z tych dwóch punktów wybrać? Oczywiście ten leżący bliżej idealnego okręgu. Na rysunku wprowadzono punkt M, leżący dokładnie pośrodku punktów E oraz SE. Zatem jeżeli okrąg przecina się nad punktem M to wybieramy E, jeżeli pod lub dokładnie w wybieramy SE. By efektywnie podejmować taką decyzję wprowadzimy zmienną decyzyjną d = F(x_p + 1, y_p - 0.5) = (x_p + 1)² + (y_p - 0.5)² - R²
Jeżeli d ≥ 0 to wybieramy kierunek SE.
Jeżeli d < 0 to wybieramy kierunek E.

Początkowa wartość zmiennej decyzyjnej d wynosić będzie F(x₀ + 1, y₀ - 0.5), gdzie (x₀, y₀) jest pierwszym rysowanym punktem okręgu - pierwszy rysujemy punkt na samym szczycie okręgu zatem (x₀, y₀) = (0, R), podstawiając to do przedstawionego wzoru otrzymujemy:
F(0 + 1, R - 0.5) = 1 + (R² - R + 0.25) - R² = 1.25 - R

W zależności od wybranego ruchu (SE lub E) inaczej zmieniać będziemy aktualną wartość zmiennej decyzyjnej d

• jeżeli wybrano kierunek E, to zwiększamy jedynie x:
  d_old = (x_p + 1)² + (y_p - 0.5)² - R²
  d_new = F(x_p + 2, y_p - 0.5) = (x_p + 2)² + (y_p - 0.5)² -R² = d_old + (2x_p + 3)
  
  
• jeżeli wybrano kierunek SE, to zwiększamy x i zmniejszamy y:
  d_old = (x_p + 1)² + (y_p - 0.5)² - R²
  d_new = F(x_p + 2, y_p - 1.5) = (x_p + 2)² + (y_p - 1.5)² - R² = d_old + (2x_p - 2y_p + 5)
  
  

Ponieważ początkowa wartość zmiennej decyzyjnej d wyszła nam ułamkowa, a nam zależy na jak najszybszych obliczeniach, zamienimy ją na liczbę całkowitą (operacje na liczbach stałoprzecinkowych wykonywane są szybciej niż na liczbach zmiennoprzecinkowych). Przemnożymy zatem jej wartości przez 4 (decyzja zależy wyłącznie od znaku zmiennej decyzyjnej, dlatego możemy tak postąpić). I tak ostatecznie otrzymujemy:

• wartość początkowa: d = 5 - 4*R
• inkrementacja przy wyborze kierunku E: d = d + 8 * x + 12
• inkrementacja przy wyborze kierunku SE: d = d + 8 * (x - y) + 20

Obliczymy 5 początkowych punktów dla okręgu o promieniu R = 10 i środku we współrzędnych (0, 0).
Pierwszy punkt to (0, R) = (0, 10)
Początkowa wartość zmiennej decyzyjnej d = 5 - 4*R = 5 - 40 = -35
Jej wartość jest mniejsza niż zero, a więc wybieramy kierunek E.
Zatem kolejny punkt to (0 + 1, 10) = (1, 10)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = -35 + 8 * 0 + 12 = - 23
Jej wartość jest mniejsza niż zero, a więc znów wybieramy kierunek E.
Zatem kolejny punkt to (1 + 1, 10) = (2, 10)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = -23 + 8 * 1 + 12 = - 3
Jej wartość jest mniejsza niż zero, a więc znów wybieramy kierunek E.
Zatem kolejny punkt to (2 + 1, 10) = (3, 10)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = -3 + 8 * 2 + 12 = 25
Jej wartość jest większa niż zero, więc wybieramy kierunek SE.
Zatem kolejny punkt to (3 + 1, 10 + 1) = (4, 11)
Wartość zmiennej decyzyjnej zmieniamy zgodnie ze wzorem d = 25 + 8 * (4 - 11) + 20 = -11
...

Obliczenia te należy kontynuować dopóki y > x, pamiętać też należy, że każdy obliczony punkt "potrkatować" trzeba wspomnianą już osimiokrotną symetrią.
Gdyby okrąg, który chcemy kreślić miał środek w punkcie innym niż (0, 0), obliczenia przebiegałyby identycznie jak dla okręgu o współrzednych środka (0, 0) tylko do ostatecznych punktów, które rysowalibyśmy dodalibyśmy przesunięcie równe środkowi. Tzn. dla okręgu o promieniu R = 10 i środku we współrzędnych (15, 30) otrzymalibyśmy identyczne obliczenia jak poprzednio tylko punkty, które narysowalibyśmy byłyby następujące:
(0 + 15, 10 + 30) = (15, 30)
(1 + 15, 10 + 30) = (16, 40)
(2 + 15, 10 + 30) = (17, 40)
(3 + 15, 10 + 30) = (18, 40)
(4 + 15, 11 + 30) = (19, 41)