Wpisany przez Tomasz Lubiński,
01 sierpnia 2005 01:04
Wyobraźmy sobie mały okrąg toczący się po zewnętrznej, lub wewnętrznej, powierzchni drugiego okręgu - na przykład łożysko rolkowe. Zaznaczona na jednym z okręgów kropka kreśli w powietrzu złożoną krzywą, którą nazywamy trochoidą. Dokładnie rzecz ujmując trochoida to krzywa płaska nakreślona przez punkt leżący na promieniu okręgu toczącego się po stronie wewnętrznej (wówczas mówimy, że jest to hipotrochoida lub hipocykloida), lub po stronie zewnętrznej drugiego okręgu (wówczas nazywamy ją epitrochoidą lub epicykloidą).
Rozpatrzmy najpierw przypadek pierwszy. Hipocykloida to krzywa płaska otrzymywana jako ślad punktu należącego do okręgu o promieniu r toczącego się po wewnętrznej powierzchni innego, okręgu o promieniu R. Współrzędne punktów hipocykloidy dane są układem równań:
Po zmianie parametrów, żeby zobaczyć efekt uruchom animację ponownie.
Rozpatrzmy najpierw przypadek pierwszy. Hipocykloida to krzywa płaska otrzymywana jako ślad punktu należącego do okręgu o promieniu r toczącego się po wewnętrznej powierzchni innego, okręgu o promieniu R. Współrzędne punktów hipocykloidy dane są układem równań:
x=(R-r)\cos(t)+r*\cos\left(\frac{(R-r)*t}{r}\right)\\\\
y=(R-r)\sin(t)-r*\sin\left(\frac{(R-r)*t}{r}\right)
Podstawiając za t kolejne liczby otrzymujemy współrzędne kolejnych punktów, tworzących hipocykloidę. Stosunek R/r określa symetrię otrzymanej hipocykloidy. Na rysunku zamieszczonym poniżej widzimy cykloidę, której stosunek symetrii wynosi 4.Hipocykloida wygląda następująco:
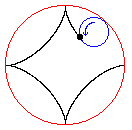
x=(R-r)\cos(t)+h*\cos\left(\frac{(R-r)*t}{r}\right)\\\\
y=(R-r)\sin(t)-h*\sin\left(\frac{(R-r)*t}{r}\right)
Te same równania dla h>r opisują hipocykloidę wydłużoną, a dla h≤r opisują hipocykloidę skróconą. Zauważmy, że dla h=0 otrzymujemy równanie, opisujące środek okręgu, który toczy się wewnątrz drugiego okręgu. Wykorzystując, tą informację możemy stworzyć animację pokazującą rysowanie hipotrochoidy. Przykładowe hipotrochoidy
(po lewj hipocykloida wydłużona, po prawej hipocykloida skrócona):
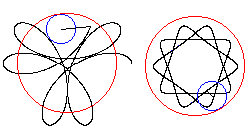
x=(R+r)\cos(t)-r*\cos\left(\frac{(R+r)*t}{r}\right)\\\\
y=(R+r)\sin(t)-r*\sin\left(\frac{(R+r)*t}{r}\right)
Epicykloida:

x=(R+r)\cos(t)-h*\cos\left(\frac{(R+r)*t}{r}\right)\\\\
y=(R+r)\sin(t)-h*\sin\left(\frac{(R+r)*t}{r}\right)
Generalnie, symetria hipocykloidy lub epicykloidy jak już wspomniałem określona jest przez stosunek długości promieni toczących się po sobie okręgów. Jej kształt zależy też wyraźnie od proporcji odległości od środka okręgu do wybranego punktu kreślącego krzywą a promieniem tego okręgu (h) - wielkość tę nazywamy "mimośrodem". Niektóre krzywe cykliczne mają znaczenie praktyczne, ich kształt mają krzywki napędzające różne mechanizmy.Przykład w JavaScript:
Po zmianie parametrów, żeby zobaczyć efekt uruchom animację ponownie.
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 3 |
| Tomasz Lubiński | JavaScript | Firefox 3.0+, Safari 3.0+, Chrome 3.0+, Opera 9.5+, IE 9.0+ | .js | .js | ***** / 1 |
Poprawiony: 01 września 2012 14:17


