Wpisany przez Tomasz Lubiński,
27 maja 2007 13:39
Załóżmy, że chcemy obliczyć całkę z funkcji f(x) w przedziale <xp; xk>. Definicja całki oznaczonej Riemana, mówi nam, że wartość całki równa jest sumie pól obszarów pod wykresem krzywej w zadanym przedziale całkowania. Sumę taką możemy obliczyć w przybliżeniu dzieląc obszar całkowania na n równych części. Dla każdej takiej części możemy wyznaczyć prostokąt, który w przybliżeniu będzie odpowiadał polu obszaru pod wykresem krzywej. Jak widać na schemacie poniżej, dla funkcji rosnącej wartości tych przybliżeń będą większe niż w rzeczywistości - nadmiar powoduje część prostokąta znajdująca się ponad wykresem krzywej - dwa pierwsze prostokąty na schemacie. Natomiast dla funkcji malejącej wartości przybliżeń będą mniejsze niż rzeczywiste pole pod wkresem - niedomiar powoduje część pola znajdująca się nad wyznaczonym prostokątem - ostatni prostokąt na schemacie.
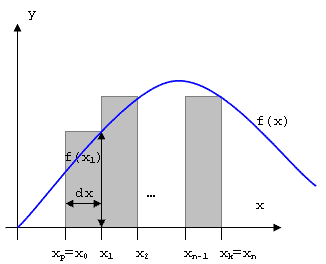
Jak już wpomnieliśmy przedział całkowania <xp; xk> podzielimy na n równych części. Szerokość każdej z nich wynosić będzie zatem:
Obliczmy najpierw szerokość przedziału dx = ( xk - xp ) / n = (5 - 2) / 3 = 3 / 3 = 1.
Teraz obliczymy wartość całki.
dx * (f( x1 ) + f( x2 ) + f( x3 )) = 1 * (f(2 + 1*1) + f(2 + 2*1) + f(2 + 3*1)) = 1 * (f(3) + f(4) + f(5)) = 1 * (12 + 19 + 28) = 59.
Zatem przybliżona wartość całki wynosi 59.

Jak już wpomnieliśmy przedział całkowania <xp; xk> podzielimy na n równych części. Szerokość każdej z nich wynosić będzie zatem:
dx = \frac{x_k - x_p}{n}
Taka też będzie szerokość każdego prostokąta przybliżającego nam wartość całki w zadanym przedziale. Wysokość każdego z prostokątów wynosić będzie:
f(x_i) \text{ dla }i = 1, 2, ..., n \text{ , gdzie } x_i = x_p + i*dx
Całkę w zadanym przedziale uzyskamy dodając do siebie pola wszystkich tych prostokątów, wynosić będzie ona zatem:
dx * f(x_1) + dx * f(x_2) + ... + dx * f(x_n) =\\\\
dx * (f(x_1) + f(x_2) + ... + f(x_n))
Warto zauważyć, iż im większa liczba przedziałów n z tym większą dokładnością wyznaczymy interesującą nas całkę.Przykład:
Obliczymy przybliżoną wartość całki dla funkcji f(x) = x2 + 3 w przedziale <2, 5> z dokładnością n = 3.Obliczmy najpierw szerokość przedziału dx = ( xk - xp ) / n = (5 - 2) / 3 = 3 / 3 = 1.
Teraz obliczymy wartość całki.
dx * (f( x1 ) + f( x2 ) + f( x3 )) = 1 * (f(2 + 1*1) + f(2 + 2*1) + f(2 + 3*1)) = 1 * (f(3) + f(4) + f(5)) = 1 * (12 + 19 + 28) = 59.
Zatem przybliżona wartość całki wynosi 59.
Przykład w JavaScript:
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C# | MS Visual Studio .net | .cs | .cs | ***** / 8 |
| Tomasz Lubiński | C/C++ | .cpp | .cpp | ***** / 13 | |
| Tomasz Lubiński | Delphi/Pascal | .pas | .pas | ***** / 4 | |
| Tomasz Lubiński | Java | .java | .java | ***** / 6 | |
| Tomasz Lubiński | JavaScript | .js | .js | ***** / 0 | |
| Jakub Konieczny | Java_Block | .jbf | .jbf | ***** / 4 |
Poprawiony: 03 grudnia 2019 09:23


