Załóżmy, że chcemy obliczyć całkę z funkcji f(x) w przedziale <x_p; x_k>. Definicja całki oznaczonej Riemana, mówi nam, że wartość całki równa jest sumie pól obszarów pod wykresem krzywej w zadanym przedziale całkowania. Sumę taką możemy obliczyć w przybliżeniu dzieląc obszar całkowania na n równych części. W metodach prostokątów i trapezów zakładaliśmy, że przybliżenie funkcji w przedziale jest funkcją liniową (przybliżenie odwzorowywało funkcję na odcinek w obrębie przedziału). W metodzie Simpsona w każdym takim przedziale będziemy przybliżać funkcję dla, której obliczamy całkę przy pomocy paraboli.


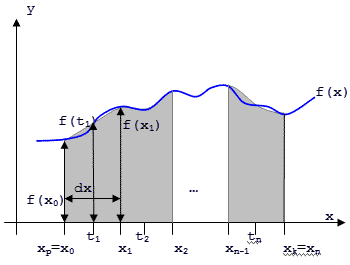
Jak już wspomnieliśmy przedział całkowania <x_p; x_k> podzielimy na n równych części. Szerokość każdej z nich wynosić będzie zatem:
Na końcach każdego przedziału funkcja będzie przyjmowała wartości f( x_i-1 ) oraz f( x_i ) dla i = 1, 2, ..., n, gdzie x_i = x_p + i*dx.
W każdym przedziale <x_i-1; x_i> funkcję f(x) będziemy przybliżać przy pomocy paraboli g(x) = a_ix² + b_ix + c_i
By jednoznacznie określić parabolę, potrzebujemy danych trzech punktów, przez które ma ona przechodzić. Dla każdego przedziału mamy dane już dwa (na końcu i początku przedziału), brakuje nam zatem jeszcze jednego. Dlatego teżdla każdego takiego przedziału wprowadzimy punkt środkowy t_i = (x_i-1 + x_i) / 2

Pole pod parabolą obliczmy z definicji całki Newtona-Leibniza, która mówi, że całka oznaczona z funkcji w przedziale zamkniętym określona jest jako różnica wartości funkcji pierwotnej na końcu tego przedziału i wartości funkcji pierwotnej na początku tego przedziału. Funkcja pierwotna dla funkcji f(x), to taka funkcja F(x), że jej pochodna równa jest funkcji f(x), czyli F'(x) = f(x). Zatem Stosując podane twierdzenie do naszego przybliżenia g(x) otrzymamy:

\int_{x_{i-1}}^{x_{i}}{g_{i}(x)dx}=G_{i}(x_{i})-G_{i}(x_{i-1})

Podstawiając funkcję pierwotną:

\int_{x_{i-1}}^{x_{i}}{g_{i}(x)dx}=\frac{a_{i}}{3}x_{i}^{3}+\frac{b_{i}}{2}x_{i}^{2}+c_{i}x_{i}-\frac{a_{i}}{3}x_{i-1}^{3}-\frac{b_{i}}{2}x_{i-1}^{2}-c_{i}x_{i-1}

Po pogrupowaniu:

\int_{x_{i-1}}^{x_{i}}{g_{i}(x)dx}=\frac{a_{i}}{3}(x_{i}^{3}-x_{i-1}^{3})+\frac{b_{i}}{2}(x_{i}^{2}-x_{i-1}^{2})+c_{i}(x_{i}-x_{i-1})

Po wyciągnięciu części wspólnej przed nawias:

\int_{x_{i-1}}^{x_{i}}{g_{i}(x)dx}=\frac{(x_{i}-x_{i-1})}{6}(2a_{i}(x_{i}^{2}+x_{i}x_{i-1}+x_{i-1}^{2})+3b_{i}(x_{i}+x_{i-1})+6c_{i})

Co po odpowiednich przekształceniach możemy sprowadzić do postaci:

\int_{x_{i-1}}^{x_{i}}{g_{i}(x)dx}=\\\frac{(x_{i}-x_{i-1})}{6}((a_{i}x_{i-1}^2+b_{i}x_{i-1}+c_{i})+(a_{i}x_{i}^2+b_{i}x_{i}+c_{i})+4(a_{i}t_{i}^2+b_{i}t_{i}+c_{i}))

Można zauważyć, że odpowiednie części równania są wartościami funkcji f:

\int_{x_{i-1}}^{x_{i}}{g_{i}(x)dx}=\frac{(x_{i}-x_{i-1})}{6}(f(x_{i-1})+f(x_{i})+4f(t_{i}))

Powyższy wzór podaje nam wartość przybliżonej całki w przedziale. Teraz trzeba dodać do siebie wartości, wszystkich przedziałów i tym sposobem otrzymamy wzór na obliczenie przybliżonej całki metodą Simpsona:

\int_{x_{p}}^{x_{k}}{f(x)dx}\approx\frac{(x_{k}-x_{p})}{6n}(f(x_{0})+f(x_{n})+2\sum_{i=1}^{n-1}{f(x_{i})}+4\sum_{i=1}^{n}{f(t_{i})})

Obliczymy przybliżoną wartość całki dla funkcji f(x) = x² + 3 w przedziale <2, 5> z dokładnością n = 3.
((x_k-x_p)/6n) * (f(x₀) + f(x_n) + 2*(f(x₁) + f(x₂)) + 4*(f(t₁) + f(t₂) + f(t₃))) = ((5-2)/(6*3)) * (f(2) + f(5) + 2*(f(3) + f(4)) + 4*(f(2.5) + f(3.5) + f(4.5))) = 3/18 * (7 + 28 + 2*(12+19) + 4*(9.25+15.25+23.25)) = 3/18 * (7 + 28 + 62 + 191) = 3/18 * 288 = 48
Zatem przybliżona wartość całki wynosi 48. Co więcej w tym wypadku możemy powiedzieć nawet, że jest to wartość dokładna ponieważ obliczaliśmy całkę dla funkcji kwadratowej (algorytm przybliżał parabolę za pomocą paraboli, a więc zrobił to dokładnie).

Funkcja f(x):
Początek przedziału całkowania:
Koniec przedziału całkowania:
Dokładność całkowania: