Wpisany przez Michał Ładanowski,
28 lutego 2011 20:32
Gdy nasza znajomość funkcji ogranicza się do zbioru argumentów oraz odpowiadającego mu zbioru wartości to aby znaleźć wartości funkcji pomiędzy znanymi nam argumentami korzystamy z interpolacji. Szukanie wartości poza obszarem obejmującym zbiór argumentów nazywamy ekstrapolacją.
Innymi słowy nasza znajomość funkcji ogranicza się do postaci stabelaryzowanej:
xi – węzły interpolacji
Cel: znalezienie wartości funkcji pomiędzy węzłami (interpolacja).
Jednym ze sposobów na osiągnięcie naszego celu jest interpolacja za pomocą wielomianów:
Nasza tabela wyznacza wielomian stopnia n-1:
Tak przygotowany układ można rozwiązać np. metodą eliminacji Gaussa.
Warto wspomnieć, że choć na ludzki rozum wydaję się, że im więcej węzłów tym lepiej, w rzeczywistości może prowadzić to jednak do znacznych wahań między węzłami – tzw. Oscylacje Rungego.
Załóżmy, że znamy 6 wartości funkcji:
Zatem będziemy obliczać układ 6 równań z 6 niewiadomymi.
a525 + a424 + a323 + a222 + a12 + a0 = 0
a535 + a434 + a333 + a232 + a13 + a0 = 2
a565 + a464 + a363 + a262 + a16 + a0 = 3
a575 + a474 + a373 + a272 + a17 + a0 = 5
a585 + a484 + a383 + a282 + a18 + a0 = 1
a5105 + a4104 + a3103 + a2102 + a110 + a0 = 2
Rozwiązaniem takiego układu są natępujące wartości:
a0 = -149.0000000000012
a1 = 178.68333333333408
a2 = -77.8583333333334
a3 = 15.566666666666668
a4 = -1.4416666666666667
a5 = 0.05
Zatem wielomian, z którego obliczać będziemy interpolowane wartości będzie miał postać:
0.05x5 + -1.4416666666666667x4 + 15.566666666666668x3 + -77.8583333333334x2 + 178.68333333333408x - 149.0000000000012
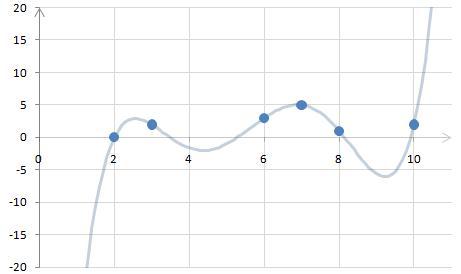
Poniżej przedstawiono wartości obliczonego wielomianu, oraz punkty na podstawie, których został on obliczony.
Innymi słowy nasza znajomość funkcji ogranicza się do postaci stabelaryzowanej:
| x1 | x2 | ... | xn |
| f(x1) | f(x2) | ... | f(xn) |
xi – węzły interpolacji
Cel: znalezienie wartości funkcji pomiędzy węzłami (interpolacja).
Jednym ze sposobów na osiągnięcie naszego celu jest interpolacja za pomocą wielomianów:
Nasza tabela wyznacza wielomian stopnia n-1:
a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + ... + a_1x + a_0
Czyli aby wyliczyć wartości funkcji pomiędzy węzłami potrzebujemy współczynników tego wielomianu, które łatwo otrzymamy podstawiając do wielomianu informacje z tabeli co stworzy nam układ równań, który zapisany w postaci macierzowej przyjmuje postać:
\begin{vmatrix}
x_{1}^{n-1}&x_{1}^{n-2}&...&x_{1}&1\\
x_{2}^{n-1}&x_{2}^{n-2}&...&x_{2}&1\\
...&...&...&...&\\
x_{n}^{n-1}&x_{n}^{n-2}&...&x_{n}&1
\end{vmatrix}
\begin{vmatrix}
a_{n-1}\\
a_{n-1}\\
...\\
a_{0}\\
\end{vmatrix}
=
\begin{vmatrix}
f(x_{1})\\
f(x_{2})\\
...\\
f(x_{n})\\
\end{vmatrix}
Warto wspomnieć, że choć na ludzki rozum wydaję się, że im więcej węzłów tym lepiej, w rzeczywistości może prowadzić to jednak do znacznych wahań między węzłami – tzw. Oscylacje Rungego.
Przykład:
Załóżmy, że znamy 6 wartości funkcji:
| xi | 2 | 3 | 6 | 7 | 8 | 10 |
| f(xi) | 0 | 2 | 3 | 5 | 1 | 2 |
Zatem będziemy obliczać układ 6 równań z 6 niewiadomymi.
a525 + a424 + a323 + a222 + a12 + a0 = 0
a535 + a434 + a333 + a232 + a13 + a0 = 2
a565 + a464 + a363 + a262 + a16 + a0 = 3
a575 + a474 + a373 + a272 + a17 + a0 = 5
a585 + a484 + a383 + a282 + a18 + a0 = 1
a5105 + a4104 + a3103 + a2102 + a110 + a0 = 2
Rozwiązaniem takiego układu są natępujące wartości:
a0 = -149.0000000000012
a1 = 178.68333333333408
a2 = -77.8583333333334
a3 = 15.566666666666668
a4 = -1.4416666666666667
a5 = 0.05
Zatem wielomian, z którego obliczać będziemy interpolowane wartości będzie miał postać:
0.05x5 + -1.4416666666666667x4 + 15.566666666666668x3 + -77.8583333333334x2 + 178.68333333333408x - 149.0000000000012
Poniżej przedstawiono wartości obliczonego wielomianu, oraz punkty na podstawie, których został on obliczony.

Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Michał Ładanowski | Java | .java | .java | ***** / 7 |
Poprawiony: 02 października 2012 17:28


