Wpisany przez Tomasz Lubiński,
08 sierpnia 2005 21:18
Metoda ta pozwala obliczyć miejsca zerowe funkcji nieliniowych w przedziałach, musi ona jednak spełniać następujące warunki:
Metoda przebiega następująco: badamy znaki pierwszej i drugiej pochodnej w badanym przedziale <a, b>. Jeżeli są one równe wówczas x(0) = a, a wzór na kolejne punkty wygląda następująco:
Po pewnej liczbie kroków albo otrzymujemy pierwiastek dokładny albo ciąg przedziałów zbieżny do pierwiastka. Metoda ta jest szybciej zbieżna niż metoda połowienia. Maksymalny błąd i-tego przybliżenia to:
- funkcja f oraz jej pierwsza i druga pochodna są ciągłe w badanym przedziale <a, b>,
- wewnątrz <a, b> znajduje się dokładnie jeden pierwiastek,
- f(a)*f(b) < 0,
- pierwsza i druga pochodna mają stały znak w badanym przedziale <a, b>.
Metoda przebiega następująco: badamy znaki pierwszej i drugiej pochodnej w badanym przedziale <a, b>. Jeżeli są one równe wówczas x(0) = a, a wzór na kolejne punkty wygląda następująco:
x^{(i)} = x^{(i-1)} - \frac{f(x^{(i-1)})}{f(b)-f(x^{(i-1)})}(b-x^{(i-1)})
w przeciwnym wypadku: x(0) = b, a wzór na kolejne punkty wygląda następująco:
x^{(i)} = x^{(i-1)} - \frac{f(x^{(i-1)})}{f(a)-f(x^{(i-1)})}(a-x^{(i-1)})
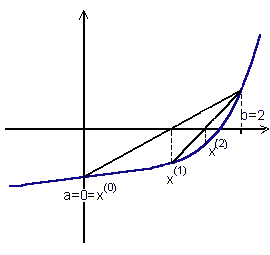
Geometryczną konstrukcję kolejnych przybliżeń pierwiastków obrazuje poniższy wykres (z którego można zresztą powyższe zależności wyznaczyć).
Po pewnej liczbie kroków albo otrzymujemy pierwiastek dokładny albo ciąg przedziałów zbieżny do pierwiastka. Metoda ta jest szybciej zbieżna niż metoda połowienia. Maksymalny błąd i-tego przybliżenia to:
\frac{f(x^{(i)})}{\min x \in <a, b> |f'(x)|}
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C/C++ | .cpp | .cpp | ***** / 5 | |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 1 |
| Tomasz Lubiński | Java | .java | .java | ***** / 3 |
Poprawiony: 27 września 2012 21:05


