Wpisany przez Marcin Ant,
15 marca 2006 20:08
Warunek brzegowy Dirichleta
Jeżeli funkcja u(x, y) jest poszukiwana na obszarze R, wówczas musi mieć zdefiniowane warunki w postaci funkcji g(x, y) na brzegu S.
u(x, y) - poszukiwana funkcja w punktach wewnątrz obszaru R,
g(x, y) - zadana funkcja dla punktów (x, y) należących do brzegu S obszaru R.
Warunek brzegowy Neumanna
lewa strona równania - pochodna normalna poszukiwanej funkcji w punktach należących do brzegu S obszaru R,
g(x, y) - zadana funkcja dla punktów (x, y) należących do brzegu S obszaru R.
Oznacza to, że na brzegu obszaru zmienność funkcji u(x, y) w kierunku normalnym dla punktów (x, y) należących do S jest równa funkcji g(x, y).
Dla zmiennej x
Aby rozwiązać równanie cząstkowe eliptycznym zastosujemy metodę różnic skończonych MRS.
Zdefiniujemy krok całkowania:
Umieśćmy siatkę na obszarze R poprzez narysowanie pionowych i poziomych linii przechodzących przez punkty (xi, yj), takich że:

Podstawiając wzory (1) oraz (2) do równania Poissona i za (xi, yj) = wij, dokonując przekształceń otrzymujemy:
Analizując powyższe równanie można zauważyć, że w celu wyznaczenia przybliżenia rozwiązania w punkcie (xi, yj), potrzebne są wartości przybliżenia rozwiązania w czterech sąsiednich punktach.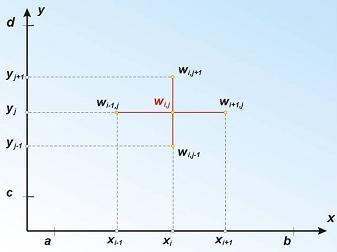
Równanie powyższe można przedstawić w postaci iteracyjnej, wyprowadzając wij z każdego równania, gdzie l oznacza numer iteracji:
Jeżeli funkcja u(x, y) jest poszukiwana na obszarze R, wówczas musi mieć zdefiniowane warunki w postaci funkcji g(x, y) na brzegu S.
u(x, y) = g(x, y) \text{, dla } (x, y) \in S

u(x, y) - poszukiwana funkcja w punktach wewnątrz obszaru R,
g(x, y) - zadana funkcja dla punktów (x, y) należących do brzegu S obszaru R.
Warunek brzegowy Neumanna
\frac{\partial u}{\partial n}(x,y)=g(x,y) \text{, dla } (x, y) \in S
gdzie:lewa strona równania - pochodna normalna poszukiwanej funkcji w punktach należących do brzegu S obszaru R,
g(x, y) - zadana funkcja dla punktów (x, y) należących do brzegu S obszaru R.
Oznacza to, że na brzegu obszaru zmienność funkcji u(x, y) w kierunku normalnym dla punktów (x, y) należących do S jest równa funkcji g(x, y).
Dla zmiennej x
\frac{u(x,y) - u(x-h,y)}{h}=g(x,y)
Dla zmiennej y
\frac{u(x,y) - u(x,y-h)}{h}=g(x,y)
Równania różniczkowe cząstkowe eliptyczne znane jako równanie Poissona, dla dwóch wymiarów i prostokątnego układu współrzędnych przyjmuje postać:
\nabla ^2 u(x,y)=\frac{d^2u}{dx^2}(x,y)+\frac{d^2u}{dy^2}(x,y)=f(x,y)
Szczególnym przypadkiem równania Poissona gdy f(x, y) = 0 jest równanie Laplace'a.Aby rozwiązać równanie cząstkowe eliptycznym zastosujemy metodę różnic skończonych MRS.
Zdefiniujemy krok całkowania:
h = \frac{b-a}{b}\\\\
k = \frac{c-d}{m}
Dzięki temu możemy podzielić: przedział [a, b] na n równych części o szerokości h oraz przedział [c, d] na m równych części o szerokości k.Umieśćmy siatkę na obszarze R poprzez narysowanie pionowych i poziomych linii przechodzących przez punkty (xi, yj), takich że:

x_i = a + ih \text{, dla } i = 0,1, .. n\\\\
y_j = c + jh \text{, dla } j = 0,1, .. m
Dla zmiennej x
\frac{\partial^2u}{\partial x^2}(x_i,y_j)=\frac{u(x_{i+1},y_j)-2u(x_i,y_j)+u(x_{i-1},y_j)}{h^2} \text{ (1) }
Dla zmiennej y
\frac{\partial^2u}{\partial y^2}(x_i,y_j)=\frac{u(x_i,y_{j+1})-2u(x_i,y_j)+u(x_i,y_{j-1})}{k^2} \text{ (2) }
Postać tą otrzymujemy po rozwinięcia funkcji f w szereg Taylora 3 rzędu w otoczeniu punktu x0 dla punktów x0+h oraz x0-h, zakładając, że f jest 4-krotnie różniczkowalna na przedziale [x0-h, x0+h]Podstawiając wzory (1) oraz (2) do równania Poissona i za (xi, yj) = wij, dokonując przekształceń otrzymujemy:
2\left(\left(\frac{h}{k}\right)^2+1\right)w_{i,j}-(w_{i+1,j} + w_{i-1,j}) - \left(\frac{h}{k}\right)^2(w_{i,j+1} + w_{i,j-1})=-h^2f(x_i,y_j)
dla i = 1,2 ... n-1 oraz j = 1,2, ... m-1Analizując powyższe równanie można zauważyć, że w celu wyznaczenia przybliżenia rozwiązania w punkcie (xi, yj), potrzebne są wartości przybliżenia rozwiązania w czterech sąsiednich punktach.

Równanie powyższe można przedstawić w postaci iteracyjnej, wyprowadzając wij z każdego równania, gdzie l oznacza numer iteracji:
w^{(l+1)}_{ij} = \frac{-h^2 f(x_i,y_j) + (w_{i+1,j}^{(l)}+w_{i-1,j}^{(l)}+w_{i,j+1}^{(l)}+w_{i,j-1}^{(l)})}{4}
dla równych kroków h = kotrzymujemy bardziej skrócony wzór na obliczenie równania Poissona:
w^{(l+1)}_{ij} = \frac{-h^2 f(x_i,y_j) + (w_{i+1,j}^{(l)}+w_{i-1,j}^{(l)})+\left(\frac{h}{k}\right)^2(w_{i,j+1}^{(l)}+w_{i,j-1}^{(l)})}{2\left(\left(\frac{h}{k}\right)^2+1\right)}
W załączonej implementacji przedstawiono rozkład temperatury w stanie ustalonym dla cienkiej kwadratowej metalowej płytki.
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Marcin Ant | Delphi/Pascal | Borland Delphi 7 | .pas | .pas | ***** / 3 |
Poprawiony: 29 września 2012 16:29


