Wpisany przez Tomasz Lubiński,
06 czerwca 2012 14:21
Zwykłe zdjęcia robione z daleka i obejmujące dużą powierzchnię są z reguły w całości ostre. Natomiast zdjęcia makro, robione z bliska miniaturowym makietom są "ostre" tylko w pewnym zakresie. Efekt taki można uzyskać dla rzeczywistych obiektów fotografując je przy użyciu obiektywów Tilt-Shift, w których użytkownik ma możliwość przesunięcia osi optycznej. Obecnie dzięki cyfrowemu przetwarzaniu obrazów taki efekt można uzyskać ze zwykłego zdjęcia bez potrzeby używania drogich i specjalistycznych obiektywów.
By uzyskać efekt makiety wystarczy wziąć zwykłe zdjęcie, które w całości jest ostre. Następnie wybrać niewielki obszar, który pozostawimy ostrym a resztę rozmyć. Na większości zdjęć odległość obiektów zmienia się w osi pionowej, tzn. obiekty znajdujące się blisko są na dole zdjęcia, a te które są dalej są wyżej. Dlatego też obszar ostrego obrazu jest poziomy, gdyż ma objąć obiekty, które są w tej samej odległości. Sposób postępowania pokazany jest na schemacie poniżej.
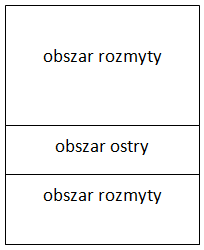
Algorytm działać będzie następująco:
Do operacji rozmywania użyjemy filtru Gaussa (rozmywania Gaussowskiego). Filtr ten zastosujemy dwa razy. Pierwszy raz w kierunku poziomym podczas kopiowania punktów z obrazu wejściowego, drugi raz w kierunku pionowym na obrazie wyjściowym. Kolejne współczynniki filtru x = 0, 1, 2, ... opisane są następującym wzorem:
Filtr modyfikuje punkty zgodnie ze wzorem:
Tak więc na przykład dla σ = 0.5 będziemy mieć następujące 3 współczynniki (czwarty współczynnik jest już mniejszy niż 0.003): 0.569917543, 0.205425518, 0.009620142. Co dla rozmycia w poziomie punktu o współrzędnych (x, y) wykorzystamy następująco:
(x, y) = (0.569917543*(x, y) + 0.205425518*(x-1, y) + 0.205425518*(x+1, y) + 0.009620142*(x-2, y) + 0.009620142*(x+2, y)) / (0.569917543 + 2*0.205425518 +2*0.009620142)
Przy czym należy zabezpieczyć się przed wyjściem poza obszar, i tak:
Podobnie dla przetwarzania w pionie.
To już wszystkie operacje jakie są konieczne do przetworzenia zwykłego zdjęcia w obraz makiety. Czasem dla lepszego efektu zwiększa się jeszcze kontrast, ale nie jest to konieczne.
Poniżej zdjęcie oryginalne:
Zdjęcie po użyciu efektu Tilt-Shift:
Ustaw ścieżkę do pliku (lub pozostaw tą domyślną), wczytaj plik a następnie kliknij na obrazie by sprawdzić działanie metody.
Ze względu na zabezpieczenia w przeglądarkach, skrypt otwiera wyłącznie pliki graficzne w obrębie naszego serwisu, np:
http://www.algorytm.org/images/stories/po/poznan2.jpg
http://www.algorytm.org/images/stories/po/poznan3.jpg
By uzyskać efekt makiety wystarczy wziąć zwykłe zdjęcie, które w całości jest ostre. Następnie wybrać niewielki obszar, który pozostawimy ostrym a resztę rozmyć. Na większości zdjęć odległość obiektów zmienia się w osi pionowej, tzn. obiekty znajdujące się blisko są na dole zdjęcia, a te które są dalej są wyżej. Dlatego też obszar ostrego obrazu jest poziomy, gdyż ma objąć obiekty, które są w tej samej odległości. Sposób postępowania pokazany jest na schemacie poniżej.

Algorytm działać będzie następująco:
- skopiuj z obrazu wejściowego do obrazu wyjściowego obszar ostry ("in-focus"),
- skopiuj z obrazu wejściowego do obrazu wyjściowego pozostały obszar, rozmywając go. Przy czym rozmycie musi być tym większe, im dalej kopiowany punkt znajduje się od obszaru ostrego.
Do operacji rozmywania użyjemy filtru Gaussa (rozmywania Gaussowskiego). Filtr ten zastosujemy dwa razy. Pierwszy raz w kierunku poziomym podczas kopiowania punktów z obrazu wejściowego, drugi raz w kierunku pionowym na obrazie wyjściowym. Kolejne współczynniki filtru x = 0, 1, 2, ... opisane są następującym wzorem:
\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^{2}}{2\sigma^{2}}}
Wartość σ określa siłę rozmycia. Ja w swoim przykładzie przyjąłem wartości od 0.1 na granicy obszaru ostrego do 6 na końcu dłuższego z obszarów rozmytych. Wartości σ zmieniają się liniowo, a więc zgodnie ze wzorem:
\sigma = 0.1 + (6 - 0.1) * \frac{odległoscPunktuOdObszaruOstrego}{wielkoscDluzszegoObszaruRozmytego}
Wielkość filtra (liczbę użytych współczynników), ograniczyłem do mniejszej z dwóch liczb:
- wielkości obrazu w danym kierunku (szerokości, jeżeli filtr stosujemy poziomo, lub wysokości jeżeli filtr stosujemy pionowo),
- liczby współczynników większych równych 0.003 (użycie mniejszych współczynników, nie ma praktycznie wpływu na obraz)
Filtr modyfikuje punkty zgodnie ze wzorem:
- dla rozmywania w poziomie
(x, y) = \frac{filtr[0]*(x, y) + filtr[1]*(x-1, y) + filtr[1]*(x+1, y) + filtr[2]*(x-2, y) + filtr[2]*(x+2, y) + ... }{filtr[0] + 2*filtr[1] +2*filtr[2] + ...}
- dla rozmywania w pionie
(x, y) = \frac{filtr[0]*(x, y) + filtr[1]*(x, y-1) + filtr[1]*(x, y+1) + filtr[2]*(x, y-2) + filtr[2]*(x, y+2) + ... }{filtr[0] + 2*filtr[1] +2*filtr[2] + ...}
Tak więc na przykład dla σ = 0.5 będziemy mieć następujące 3 współczynniki (czwarty współczynnik jest już mniejszy niż 0.003): 0.569917543, 0.205425518, 0.009620142. Co dla rozmycia w poziomie punktu o współrzędnych (x, y) wykorzystamy następująco:
(x, y) = (0.569917543*(x, y) + 0.205425518*(x-1, y) + 0.205425518*(x+1, y) + 0.009620142*(x-2, y) + 0.009620142*(x+2, y)) / (0.569917543 + 2*0.205425518 +2*0.009620142)
Przy czym należy zabezpieczyć się przed wyjściem poza obszar, i tak:
- jeżeli, x - indeks_wspolczynnika < 0, to zamiast tego użyjemy wartości |x - indeks_wspolczynnika|
- jeżeli, x + indeks_wspolczynnika > szerokosc_obrazu, to zamiast tego użyjemy wartości x + indeks_wspolczynnika - szerokosc_obrazu + 1
Podobnie dla przetwarzania w pionie.
To już wszystkie operacje jakie są konieczne do przetworzenia zwykłego zdjęcia w obraz makiety. Czasem dla lepszego efektu zwiększa się jeszcze kontrast, ale nie jest to konieczne.
Poniżej zdjęcie oryginalne:

Zdjęcie po użyciu efektu Tilt-Shift:

Przykład w JavaScript:
Ustaw ścieżkę do pliku (lub pozostaw tą domyślną), wczytaj plik a następnie kliknij na obrazie by sprawdzić działanie metody.
Ze względu na zabezpieczenia w przeglądarkach, skrypt otwiera wyłącznie pliki graficzne w obrębie naszego serwisu, np:
http://www.algorytm.org/images/stories/po/poznan2.jpg
http://www.algorytm.org/images/stories/po/poznan3.jpg
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C# | Visual Studio C# 2010 Express | .cs | .cs | ***** / 0 |
| Tomasz Lubiński | JavaScript | Firefox 3.0+, Safari 3.0+, Chrome 3.0+, Opera 9.5+, IE 9.0+ | .js | .js | ***** / 0 |
Poprawiony: 23 sierpnia 2012 14:40


