Wpisany przez Tomasz Lubiński,
05 kwietnia 2006 19:48
Algorytm interpolacji dwukwadratowej (ang. Biquadratic Interpolation), zwany inaczej metodą podwójnej interpolacji kwadratowej jest algorytmem służącym do zmiany wielkości obrazu (ang. resampling). Każdy piksel obrazu wynikowego przyjmuje wartość na podstawie wartości dziewięciu sąsiednich punktów obrazu wejściowego. Nazwa algorytmu bierze się z fatu, iż interpolację kwadratową przeprowadzamy dwukrotnie - jeden raz w poziome i jeden raz w pionie.
Najpierw należy obliczyć, w którym miejscu w obrazie wejściowym znajduje się rozpatrywany punkt obrazu wyjściowego. Schemat poniżej pokazuje dwa nałożone na siebie obrazy (4x4 oraz 5x5)

niech, widthsrc oraz widthdst oznaczają odpowiednio szerokość obrazu wejściowego i obrazu wyjściowego, a heightsrc oraz heightdst odpowiednio wysokość obrazu wejściowego i wyjściowego.
Przyjmiemy wówczas, że:
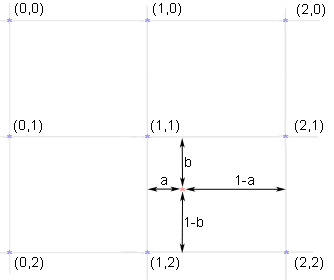
Teraz przeprowadzimy interpolację kwadratową w kierunku poziomym:
Należy przekształcić obraz 4x10 w obraz 5x16.
Obliczamy współczynniki powiększenia:
ratiox = widthsrc / widthdst = 4/5 = 0.8
ratioy = heightsrc / heightdst = 10 / 16 = 0.625
Obliczmy wartość dla punktu (3, 7).
x = i*ratiox = 3 * 0.8 = 2.4
y = j*ratioy = 7 * 0.625 = 4.375
A więc będziemy musieli wziąć pod uwagę w naszych obliczeniach wartości w punktach (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 3), (3, 4), (3, 5). Niech wartosci w tych punktach wynoszą odpowiednio: (1, 3) = 25, (1, 4) = 15, (1, 5) = 35, (2, 3) = 28, (2, 4) = 40, (2, 5) = 52, (3, 3) = 15, (3, 4) = 29, (3, 5) = 28. Obliczymy teraz współczynniki a i b - są to częsci dziesiętne odpowiednich składowych.
a = 0.375
b = 0.4
Przeprowadzimy teraz interpolację kwadratową w kierunku poziomym:
Fa,0 = F1,0 + (F2,0 - F0,0)*a + (F0,0 - 2*F1,0 + F2,0)*a*a = 28 + (15 - 25)*0.375 + (25 - 2*28 + 15)*0.375*0.375 = 28 - 3.57 - 2.25 = 22.18
Fa,1 = F1,1 + (F2,1 - F0,1)*a + (F0,1 - 2*F1,1 + F2,1)*a*a = 40 + (29 - 15)*0.375 + (15 - 2*40 + 29)*0.375*0.375 = 40 + 5.25 - 5.0625 = 40.1875
Fa,2 = F1,2 + (F2,2 - F0,2)*a + (F0,2 - 2*F1,2 + F2,2)*a*a = 52 + (28 - 35)*0,375 + (35 - 2*52 + 28)*0.375*0.375 = 52 - 2.625 - 5.765625 = 43.609375
A następnie na podstawie tych wyników w kierunku pionowym:
Fa,b = Fa,1 + (Fa,2 - Fa,0)*b + (Fa,0 - 2*Fa,1 + Fa,2)*b*b = 40.1875 + (43.609375 - 22.18)*0.4 + (22.18 - 2*40.1875 + 43.609375)*0.4*0.4 = 40.1875 + 8.571894 - 2.3337 = 46.425694
A więc wartość składowej w punkcie (3, 7) wynosić będzie 46.425694. Obliczenia takie należy powtórzyć dla wszystkich punktów i wszystkich składowych.
Schemat poniżej pokazuje zdjęcie oryginalne (na środku) powiększone czterokrotnie (po prawej) oraz pomniejszone czterokrotnie (po lewej). Algorytm interpolacji dwukwadratowej daje lepsze rezultaty niż algorytm interpolacji dwuliniowej. Wynik przy zastosowaniu interpolacji dwukwadratowej jest mniej rozmyty, ale mogą powstawać przekłamania na ostrych krawędziach w obrazie. Jeszcze lepsze rezultaty daje on jeżeli po jego wykonaniu wprowadzimy korekcję gamma dla współczynnika gamma większego od 1.

Najpierw należy obliczyć, w którym miejscu w obrazie wejściowym znajduje się rozpatrywany punkt obrazu wyjściowego. Schemat poniżej pokazuje dwa nałożone na siebie obrazy (4x4 oraz 5x5)

niech, widthsrc oraz widthdst oznaczają odpowiednio szerokość obrazu wejściowego i obrazu wyjściowego, a heightsrc oraz heightdst odpowiednio wysokość obrazu wejściowego i wyjściowego.
Przyjmiemy wówczas, że:
ratio_x = \frac{width_{src}}{width_{dst}}\\\\
ratio_y = \frac{height_{src}}{height_{dst}}
Wówczas dla każdego punktu obrazu wyjściowego (i oznacza kolumnę, j oznacza wiersz - zakładamy, że indeksy liczone są od 0 włącznie) przeprowadzamy następujące obliczenia:
x = i*ratio_x\\\\
y = j*ratio_y
Oznacza to, że dla punku o współrzędnych (i, j) obrazu wyjściowego należy użyć wartości punktu o współrzędnych (x, y) obrazu wejściowego. Przykładowe umiejscowienie tak wyliczonego punktu pokazano na schemacie poniżej. W wyjątkowej sytuacji - np. dla punktów znajdujących się na krawędziach obrazu odległość a i/lub b wynosi zero. Zuważyć należy też iż, do obliczeń w pobliżu krawędzi obrazu potrzebne będą piksle leżące poza obrazem wejściowym. Ja przyjąłem dla nich wartość piksli leżących na krawędziach.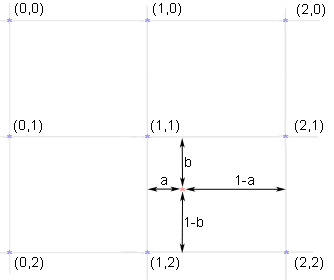
Teraz przeprowadzimy interpolację kwadratową w kierunku poziomym:
F_{a,0} = F_{1,0} + (F_{2,0} - F_{0,0})*a + (F_{0,0} - 2*F_{1,0} + F_{2,0})*a^2\\\\
F_{a,1} = F_{1,1} + (F_{2,1} - F_{0,1})*a + (F_{0,1} - 2*F_{1,1} + F_{2,1})*a^2\\\\
F_{a,2} = F_{1,2} + (F_{2,2} - F_{0,2})*a + (F_{0,2} - 2*F_{1,2} + F_{2,2})*a^2
A następnie na podstawie tych wyników w kierunku pionowym:
F_{a,b} = F_{a,1} + (F_{a,2} - F_{a,0})*b + (F_{a,0} - 2*F_{a,1} + F_{a,2})*b^2
Obliczenia takie należy przeprowadzić dla każdej składowej koloru z osobna. Po obliczeniach należy sprawdzić czy wynik mieści się w zakresie składowej, jeżeli nie to jeżeli jest on za duży to należy przyjąć możliwe maksimum, jeżeli za mały to należy przyjąć wartość możliwie najmniejszą.Przykład:
Należy przekształcić obraz 4x10 w obraz 5x16.
Obliczamy współczynniki powiększenia:
ratiox = widthsrc / widthdst = 4/5 = 0.8
ratioy = heightsrc / heightdst = 10 / 16 = 0.625
Obliczmy wartość dla punktu (3, 7).
x = i*ratiox = 3 * 0.8 = 2.4
y = j*ratioy = 7 * 0.625 = 4.375
A więc będziemy musieli wziąć pod uwagę w naszych obliczeniach wartości w punktach (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 3), (3, 4), (3, 5). Niech wartosci w tych punktach wynoszą odpowiednio: (1, 3) = 25, (1, 4) = 15, (1, 5) = 35, (2, 3) = 28, (2, 4) = 40, (2, 5) = 52, (3, 3) = 15, (3, 4) = 29, (3, 5) = 28. Obliczymy teraz współczynniki a i b - są to częsci dziesiętne odpowiednich składowych.
a = 0.375
b = 0.4
Przeprowadzimy teraz interpolację kwadratową w kierunku poziomym:
Fa,0 = F1,0 + (F2,0 - F0,0)*a + (F0,0 - 2*F1,0 + F2,0)*a*a = 28 + (15 - 25)*0.375 + (25 - 2*28 + 15)*0.375*0.375 = 28 - 3.57 - 2.25 = 22.18
Fa,1 = F1,1 + (F2,1 - F0,1)*a + (F0,1 - 2*F1,1 + F2,1)*a*a = 40 + (29 - 15)*0.375 + (15 - 2*40 + 29)*0.375*0.375 = 40 + 5.25 - 5.0625 = 40.1875
Fa,2 = F1,2 + (F2,2 - F0,2)*a + (F0,2 - 2*F1,2 + F2,2)*a*a = 52 + (28 - 35)*0,375 + (35 - 2*52 + 28)*0.375*0.375 = 52 - 2.625 - 5.765625 = 43.609375
A następnie na podstawie tych wyników w kierunku pionowym:
Fa,b = Fa,1 + (Fa,2 - Fa,0)*b + (Fa,0 - 2*Fa,1 + Fa,2)*b*b = 40.1875 + (43.609375 - 22.18)*0.4 + (22.18 - 2*40.1875 + 43.609375)*0.4*0.4 = 40.1875 + 8.571894 - 2.3337 = 46.425694
A więc wartość składowej w punkcie (3, 7) wynosić będzie 46.425694. Obliczenia takie należy powtórzyć dla wszystkich punktów i wszystkich składowych.
Schemat poniżej pokazuje zdjęcie oryginalne (na środku) powiększone czterokrotnie (po prawej) oraz pomniejszone czterokrotnie (po lewej). Algorytm interpolacji dwukwadratowej daje lepsze rezultaty niż algorytm interpolacji dwuliniowej. Wynik przy zastosowaniu interpolacji dwukwadratowej jest mniej rozmyty, ale mogą powstawać przekłamania na ostrych krawędziach w obrazie. Jeszcze lepsze rezultaty daje on jeżeli po jego wykonaniu wprowadzimy korekcję gamma dla współczynnika gamma większego od 1.

Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C/C++ | Borland Builder 6 | .cpp | .cpp | ***** / 1 |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 1 |
Poprawiony: 26 sierpnia 2012 08:46


