Wpisany przez Tomasz Lubiński,
27 lipca 2005 18:31
Boidy stworzone przez Craiga Reynoldsa, wykazują bardzo realistyczne zachowanie się stada (ptaki, ławice ryb). Przypisał on każdemu boidowi następujące reguły postępowania:
Zacznijmy jednak od początku. W przestrzeni dwuwymiarowej (a taką tutaj się zajmiemy), boid zdefiniowany jest przes 4 wartości: współrzędne x oraz y, a także prędkości dla każdego z wymiarów vx oraz vy. Uściślijmy teraz kto jest sąsiadem boida. Sąsiadami boida będziemy nazywać inne boidy (ewentualnie przeszkody, drapieżniki lub pożywienie), które znajdują się w "zakresie jego zmysłów". Czyli takie, które znajdują się w odpowiednio małej odległości (d) i jednocześnie w polu widzenia boida - który określony jest przez kąt (r). Tak więc sąsiedzi to będzie wszystko to co znajdzie się w poszarzonym polu.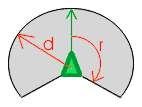
Zajmijmy się teraz pierwszym warunkiem - każdy boid dopasowywuje swoją prędkość i kierunek lotu do sąsiednich boidów.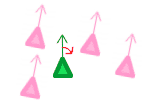
Kolejne reguły o przeszkodach, drapieżnikach i pożywieniu można wprowadzić do symulacji boidów, uwzględniając regułę o bezpiecznej odległości. Dodatkowo, w celu oddania większego realizmu, powinniśmy dodać, losowe zakłócenia ruchu boidów (np. w każdej iteracji dodając do składowych vx oraz vy niewielkiego zaburzenia). Powinniśmy też zauważyć, że każdy boid, może poruszać się z pewną maksymalną prędkością. Jeżeli prędkość boida przekroczy ją, to powinniśmy zmniejszyć jego prędkość np. o 25%.
- każdy boid dopasowywuje swoją prędkość i kierunek lotu do sąsiednich boidów,
- każdy boid stara się być w środku grupy sąsiednich boidów,
- każdy boid zachowuje bezpieczną odległość od sąsiednich boidów,
- każdy boid unika przeszkód,
- każdy boid może opuścić stado, gdy ucieka przed drapieżnikiem lub potrzebuje pożywienie.
Zacznijmy jednak od początku. W przestrzeni dwuwymiarowej (a taką tutaj się zajmiemy), boid zdefiniowany jest przes 4 wartości: współrzędne x oraz y, a także prędkości dla każdego z wymiarów vx oraz vy. Uściślijmy teraz kto jest sąsiadem boida. Sąsiadami boida będziemy nazywać inne boidy (ewentualnie przeszkody, drapieżniki lub pożywienie), które znajdują się w "zakresie jego zmysłów". Czyli takie, które znajdują się w odpowiednio małej odległości (d) i jednocześnie w polu widzenia boida - który określony jest przez kąt (r). Tak więc sąsiedzi to będzie wszystko to co znajdzie się w poszarzonym polu.

\sqrt{(e.x-b.x)^2+(e.y-b.y)^2} < d
jeżeli nie to nie sprawdzamy już dalej bo element na pewno nie jest sąsiadem boida. Jeżeli tak, to sprawdzamy, czy jest on w kącie widzenia boida. Czyli obliczamy kąt pod którym porusza się boid:
k1=\arctan \left( \frac{b.vy}{b.vx}\right)
oraz kąt odcinka od boidu do elementu,
k2=\arctan \left( \frac{e.y-b.y}{e.x-b.x}\right)
(pamiętaj o zabezpieczeniu przed dzieleniem przez 0). Teraz badamy wartość bezwzględną różnicy kątów i sprawdzamy czy jest mniejsza od r, jeżeli tak to element jest sąsiadem boida, jeżeli nie to nie jest.Zajmijmy się teraz pierwszym warunkiem - każdy boid dopasowywuje swoją prędkość i kierunek lotu do sąsiednich boidów.

b.vx=b.vx+(waga*(vx_{srednia}-b.vx))\\
b.vy=b.vy+(waga*(vy_{srednia}-b.vy))
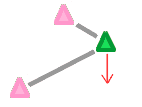
Druga reguła: każdy boid stara się być w środku grupy sąsiednich boidów.

odl = \sqrt{(s.x-b.x)^2+(s.y-b.y)^2)} \\\\
b.vx=b.vx+waga*\frac{(s.x-b.x)*(odl-odleglosc_{srednia})}{odl} \\\\
b.vy=b.vy+waga*\frac{(s.y-s.y)*(odl-odleglosc_{srednia})}{odl}
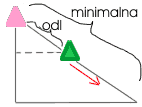
Kolejna reguła: każdy boid zachowuje bezpieczną odległość od sąsiednich boidów.

odl = \sqrt{(s.x-b.x)^2+(s.y-b.y)^2)} \\\\
b.vx=b.vx-waga*\left(\frac{(s.x-b.x)*min}{odl}-(s.x-b.x)\right) \\\\
b.vy=b.vy-waga*\left(\frac{(s.y-b.y)*min}{odl}-(s.y-b.y)\right)
gdzie min jest zadaną odległością minimalną, której nie powinien przekraczać boid.Kolejne reguły o przeszkodach, drapieżnikach i pożywieniu można wprowadzić do symulacji boidów, uwzględniając regułę o bezpiecznej odległości. Dodatkowo, w celu oddania większego realizmu, powinniśmy dodać, losowe zakłócenia ruchu boidów (np. w każdej iteracji dodając do składowych vx oraz vy niewielkiego zaburzenia). Powinniśmy też zauważyć, że każdy boid, może poruszać się z pewną maksymalną prędkością. Jeżeli prędkość boida przekroczy ją, to powinniśmy zmniejszyć jego prędkość np. o 25%.
Przykład w JavaScript:
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C/C++ | Borland Builder 6 | .cpp | .cpp | ***** / 6 |
| Tomasz Lubiński | JavaScript | Firefox 3.0+, Safari 3.0+, Chrome 5.0+, Opera 9.5+, IE 6.0+ | .js | .js | ***** / 2 |
Poprawiony: 15 sierpnia 2012 15:06



https://youtu.be/AiCFtmdrvHM?t=69
Wydaje się, że potrzebna jest centralnie przechowywana informacja o pożądanym szyku.