Wpisany przez Tomasz Lubiński,
27 lipca 2005 19:00
Mózg ludzki składa się z około 1011 elementów przetwarzających sygnały zwanych neuronami. Neuron razem ze swoimi wypustkami - dendrytami i zawsze jednym neurytem (aksonem), jest przystosowany do przewodzenia i przetwarzania, a także wytwarzania bodźców nerwowych. Charakteryzuje się tym, że przewodzi bodźce zawsze w jednym kierunku od dendrytów do ciała komórki (perikarionu) i z komórki dalej przez neuryt (wypustkę osiową). Nerony komunikują się poprzez łączącą je sieć aksonów i synaps, których jest około 1015, co daje około 104 synaps na neuron. Neuron jest podstawowym elementem biologicznej sieci neuronowej.
Pierwszą formalna definicję sztucznego neuronu opartą na uproszczonym modelu biologicznym opisanym wyżej podali McCulloch i Pitts. Zaproponowany przez nich model oparty jest na następujących zasadach. Sygnały wejściowe xi, i = 1,2,..., n mają wartość 1 lub 0, zależnie od tego czy w chwili k impuls wejściowy pojawił się, czy tez nie. Sygnał wyjściowy neuronu oznaczony jest przez y. Natomiast T określa poziom aktywacji neuronu. Reguła aktywacji ma dla tego modelu postać:
Oto najczęściej wykorzystywane funkcje przenoszenia:
Pierwszą formalna definicję sztucznego neuronu opartą na uproszczonym modelu biologicznym opisanym wyżej podali McCulloch i Pitts. Zaproponowany przez nich model oparty jest na następujących zasadach. Sygnały wejściowe xi, i = 1,2,..., n mają wartość 1 lub 0, zależnie od tego czy w chwili k impuls wejściowy pojawił się, czy tez nie. Sygnał wyjściowy neuronu oznaczony jest przez y. Natomiast T określa poziom aktywacji neuronu. Reguła aktywacji ma dla tego modelu postać:
\begin{cases}
y^{k+1}=1 & \text{ jeżeli } w_1*x_1+w_2*x_2+...+w_n*x_n \geq T\\
y^{k+1}=0 & \text{ w przeciwnym wypadku }
\end{cases}
W praktyce wykorzystuje się jednak bardziej rozwinięty model neuronu:
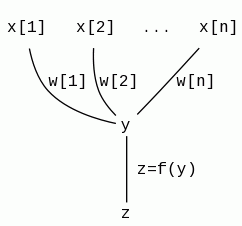
y = w_1*x_1+w_2*x_2+...+w_n*x_n
Właściwa odpowiedź neuronu z zależy od pobudzenia y zgodnie z funkcją przenoszenia (przejścia lub aktywacji) z=f(y) (tę funkcję realizuje jądro komórkowe).Oto najczęściej wykorzystywane funkcje przenoszenia:
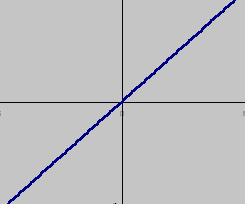
- funkcja liniowa: f(y) = ay+b,
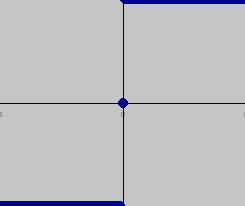
- funkcja signum: f(y) = sgn(y), (-1 dla y<0, 0 dla y=0, 1 dla y>0)
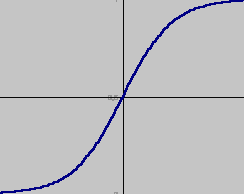
- funkcja sigmoidalna f(y) = 1/(1+exp(-y)),
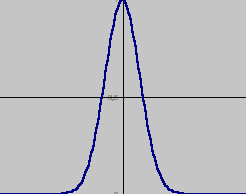
- funkcja Gaussa f(y) = exp(-y2).
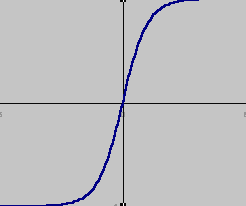
- tangens hiperboliczny f(y) = tanh(y),
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 4 |
Poprawiony: 15 sierpnia 2012 13:46


