Wpisany przez Tomasz Lubiński,
09 sierpnia 2005 19:44
Jeżeli należy wygenrować graf o zadanym ciągu stopni wierzchołków najpierw należy sprawdzić czy taki graf istnieje, czyli czy ciąg stopni jest graficzny. Można więc powiedzieć, ze dany ciąg liczb c=c1, c2, ..., cn jest graficzny jezeli istnieje graf o n wierzchołkach, dla którego c jest ciągiem stopni wierzchołków. Na przykład nie da się wygenerować grafu o 4 wierzchołkach i ciągu stopni 2,2,2,1.
Przedstawiony tutaj algorytm oparty jest o twierdzenie P. Erdos, T. Gallai z 1960 roku, które mówi, iż podział liczby 2k na n części c1 ≥ c2 ≥ ... ≥ cn jest podziałem graficznym wtedy i tylko wtedy, gdy dla każdej liczby całkowitej j z przedziału od 1 do n-1 jest spełniona nierówność.
Algorytm przebiega następująco:
Przedstawiony tutaj algorytm oparty jest o twierdzenie P. Erdos, T. Gallai z 1960 roku, które mówi, iż podział liczby 2k na n części c1 ≥ c2 ≥ ... ≥ cn jest podziałem graficznym wtedy i tylko wtedy, gdy dla każdej liczby całkowitej j z przedziału od 1 do n-1 jest spełniona nierówność.
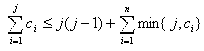
Algorytm przebiega następująco:
- Sprawdź czy suma elementów ciągu jest liczbą parzystą? Jeśli nie to ciąg nie jest graficzny.
- Posortuj ciąg c nierosnąco.
- Dla każdego j=1, 2, ..., n-1 sprawdź czy spełniona jest nierówność twierdzenia P. Erdos, T. Gallai (1960).
- Jeżeli istnieje takie j, że nierówność jest spełniona, to zadany ciąg stopni wierzchołków c nie jest graficzny.
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C/C++ | .cpp | .cpp | ***** / 2 | |
| Tomasz Lubiński | Delphi/Pascal | .pas | .pas | ***** / 1 | |
| Tomasz Lubiński | Java | .java | .java | ***** / 1 |
Poprawiony: 17 sierpnia 2012 15:28



Prosty dowód tw. Erdos i Galai podał Choudun w Bull. Austial. Math. Soc. vol.33 (1986), 67-70.