Wpisany przez Tomasz Lubiński,
16 czerwca 2007 14:46
Opisana w tym artykule metoda została opracowana przeze mnie w ramach mojej pracy magisterskiej
pt: "Algorytmy wyznaczania niepewnych pozycji na morzu". Została ona opisana dla obliczeń
przeprowadzonych na akwenach wodnych, ale z powodzeniem może być stosowana do wyznaczenia
obszaru poszukiwań na lądzie - wówczas wyspy oznaczać będą przeszkody terenowe.
Zaproponowana metoda do przeprowadzenia obliczeń wymaga znajomości ukształtowania basenów morskich. Linie brzegowe reprezentowane są przez wielokąty, będące zbiorem punktów:
p0i, p1i, ... pni - punkty wyznaczające i-tą linię brzegową, położenie każdego punktu opisane jest przez długość i szerokość geograficzną.
Oprócz linii brzegowych proponowana metoda wyznaczania pozycji niepewnej wymaga następujących danych wejściowych:
Dane wejściowe, oraz pierwsze trzy kroki metody zapożyczone zostały z algorytmu opisanego przez mojego promotora dr inż. Mikołaja Sobczaka w pracy “Determining uncertain position of the ship”.
Krok 1.
W pierwszym kroku wyznaczony zostaje okrąg pozycyjny określający niepewną pozycję jednostki dla pełnego morza (bez linii brzegowej). Promień tego okręgu obliczany jest z następującego wzoru:
W kroku drugim wyselekcjonowane są wszystkie punkty bazowe. Są to wszystkie punkty, które leżą wewnątrz okręgu pozycyjnego. Odcinek linii brzegowej wyznaczony przez dwa punkty bazowe nazywamy odcinkiem bazowym.
Krok 3.
Dla wszystkich wektorów niebędących wektorami bazowymi wyznaczone zostają punkty przecięcia z okręgiem pozycyjnym wyznaczonym w kroku 1. Punkty przecięcia znajdujące się na odcinku linii brzegowej wyznaczonej przez jeden punkt bazowy i jeden punkt nie bazowy noszą nazwę punktów dodatkowych. Natomiast punkty znajdujące się na odcinku linii brzegowej wyznaczonej przez dwa punkty nie bazowe noszą nazwę punktów specjalnych.
Rezultat działania pierwszych trzech kroków algorytmu został zaprezentowany na schemacie poniżej. Na czerwono zostały przedstawione punkty bazowe, na zielono punkty dodatkowe oraz na niebiesko punkty specjalne.
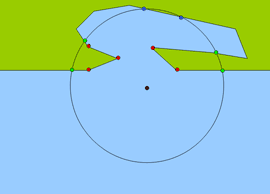
Krok 4.
Dla wszystkich punktów bazowych, specjalnych oraz dodatkowych sprawdzana jest możliwość bezpośredniego osiągnięcia tego punktu z punktu centralnego. Pozycja jest bezpośrednio osiągalna wówczas, gdy odcinek łączący ją z punktem bazowym nie przecina się żadnym innym odcinkiem tworzącym linie brzegową. Wszystkie punkty, do których dopłynąć można bezpośrednio z punktu centralnego tworzą zbiór punktów osiągalnych. Na schemacie poniżej wszystkie punkty osiągalne połączone są odcinkiem z punktem centralnym.
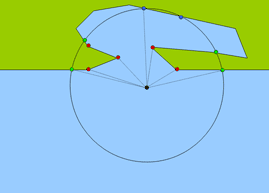
Krok 5.
Jeżeli dwa kolejne punkty osiągalne tworzą odcinek, to wówczas do wyniku dodajemy trójkąt o wierzchołkach leżących we współrzędnych tych dwóch punktów oraz punkcie centralnym. Na schemacie poniżej pokazano rezultat dodania do wyniku wyżej zdefiniowanych trójkątów.
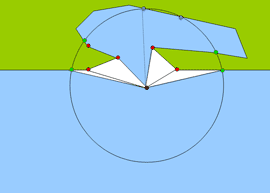
Krok 6.
Jeżeli dwa kolejne punkty należące do uporządkowanego zbioru punktów osiągalnych nie należą do zbioru punktów bazowych i nie tworzą one linii brzegowej, to rozpinamy pomiędzy nimi wycinek kołowy. Podobnie postępujemy dla pozostałych par punktów, które nie tworzą odcinka linii brzegowej, a promienie wodzące okręgu pozycyjnego oparte na tych punktach nie przecinają się z żadną linią brzegową. Na kolejnym schemacie pokazano rezultat dodania wycinków kołowych zdefiniowanych w powyższych aksjomatach.
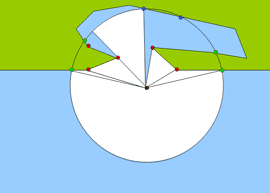
Krok 7.
Jeżeli dwa kolejne punkty z uporządkowanego zbioru punktów osiągalnych nie tworzą linii brzegowej i przynajmniej jeden z promieni wodzących okręgu pozycyjnego opartego na tych punktach przecina się z linią brzegową, to wówczas do wyniku wstawiamy dodatkowy trojkąt.Na kolejnym schemacie pokazano wynik metody po wprowadzeniu dodatkowych trójkątów.

Krok 8.
W kolejnym kroku wywołujemy rekurencyjnie metodę dla wszystkich punktów po wypłynięciu, zza których jednostka może kontynuować rejs. Wywołanie rekurencyjne następuje dla wartości promienia pomniejszonego o przebytą już drogę. W celu zmniejszenia liczby wywołań, każda rekurencyjnie wywołana funkcja zapamiętuje punkty, dla których została już wywołana, tak by nie wywoływać jej ponownie dla tego samego punktu. Na schemacie poniżej strzałkami zaznaczono miejsca, w których nastąpi rekurencyjne wywołanie metody.
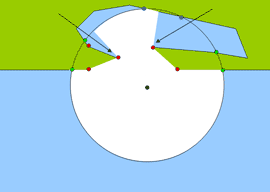
Wyniki działania metody dla wywołań rekurencyjnych należy dodać do ostatecznego rezultatu metody. W ten sposób ze złożenia trójkątów i wycinków kołowych powstaje powierzchnia wewnątrz której znajduje się poszukiwana jednostka. Wynik działania metody naniesiony jest na schemacie poniżej.
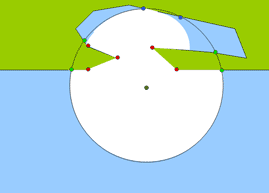
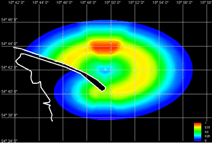
Opisany powyżej algorytm w pracy magisterskiej został wzbogacony o dodatkowe dane i wykorzystany do obliczenia prawdopodieństwa położenia jednostki w danym miejscu:
Zaproponowana metoda do przeprowadzenia obliczeń wymaga znajomości ukształtowania basenów morskich. Linie brzegowe reprezentowane są przez wielokąty, będące zbiorem punktów:
P_i = <p_0^i, p_1^i, ..., p_n^i>
gdzie:p0i, p1i, ... pni - punkty wyznaczające i-tą linię brzegową, położenie każdego punktu opisane jest przez długość i szerokość geograficzną.
Oprócz linii brzegowych proponowana metoda wyznaczania pozycji niepewnej wymaga następujących danych wejściowych:
- szerokość i długość geograficzna ostatniej znanej pozycji statku, zwana dalej punktem centralnym,
- ts - znacznik czasowy ostatniej znanej pozycji statku, przekazanej przez samą jednostkę lub pochodzącą ze źródeł zewnętrznych,
- tn - aktualny znacznik czasowy,
- vmax - maksymalna prędkość poszukiwanej jednostki.
Dane wejściowe, oraz pierwsze trzy kroki metody zapożyczone zostały z algorytmu opisanego przez mojego promotora dr inż. Mikołaja Sobczaka w pracy “Determining uncertain position of the ship”.
Krok 1.
W pierwszym kroku wyznaczony zostaje okrąg pozycyjny określający niepewną pozycję jednostki dla pełnego morza (bez linii brzegowej). Promień tego okręgu obliczany jest z następującego wzoru:
r = (t_n - t_s)*v_{max}
Krok 2.W kroku drugim wyselekcjonowane są wszystkie punkty bazowe. Są to wszystkie punkty, które leżą wewnątrz okręgu pozycyjnego. Odcinek linii brzegowej wyznaczony przez dwa punkty bazowe nazywamy odcinkiem bazowym.
Krok 3.
Dla wszystkich wektorów niebędących wektorami bazowymi wyznaczone zostają punkty przecięcia z okręgiem pozycyjnym wyznaczonym w kroku 1. Punkty przecięcia znajdujące się na odcinku linii brzegowej wyznaczonej przez jeden punkt bazowy i jeden punkt nie bazowy noszą nazwę punktów dodatkowych. Natomiast punkty znajdujące się na odcinku linii brzegowej wyznaczonej przez dwa punkty nie bazowe noszą nazwę punktów specjalnych.
Rezultat działania pierwszych trzech kroków algorytmu został zaprezentowany na schemacie poniżej. Na czerwono zostały przedstawione punkty bazowe, na zielono punkty dodatkowe oraz na niebiesko punkty specjalne.

Krok 4.
Dla wszystkich punktów bazowych, specjalnych oraz dodatkowych sprawdzana jest możliwość bezpośredniego osiągnięcia tego punktu z punktu centralnego. Pozycja jest bezpośrednio osiągalna wówczas, gdy odcinek łączący ją z punktem bazowym nie przecina się żadnym innym odcinkiem tworzącym linie brzegową. Wszystkie punkty, do których dopłynąć można bezpośrednio z punktu centralnego tworzą zbiór punktów osiągalnych. Na schemacie poniżej wszystkie punkty osiągalne połączone są odcinkiem z punktem centralnym.

Krok 5.
Jeżeli dwa kolejne punkty osiągalne tworzą odcinek, to wówczas do wyniku dodajemy trójkąt o wierzchołkach leżących we współrzędnych tych dwóch punktów oraz punkcie centralnym. Na schemacie poniżej pokazano rezultat dodania do wyniku wyżej zdefiniowanych trójkątów.

Krok 6.
Jeżeli dwa kolejne punkty należące do uporządkowanego zbioru punktów osiągalnych nie należą do zbioru punktów bazowych i nie tworzą one linii brzegowej, to rozpinamy pomiędzy nimi wycinek kołowy. Podobnie postępujemy dla pozostałych par punktów, które nie tworzą odcinka linii brzegowej, a promienie wodzące okręgu pozycyjnego oparte na tych punktach nie przecinają się z żadną linią brzegową. Na kolejnym schemacie pokazano rezultat dodania wycinków kołowych zdefiniowanych w powyższych aksjomatach.

Krok 7.
Jeżeli dwa kolejne punkty z uporządkowanego zbioru punktów osiągalnych nie tworzą linii brzegowej i przynajmniej jeden z promieni wodzących okręgu pozycyjnego opartego na tych punktach przecina się z linią brzegową, to wówczas do wyniku wstawiamy dodatkowy trojkąt.Na kolejnym schemacie pokazano wynik metody po wprowadzeniu dodatkowych trójkątów.

Krok 8.
W kolejnym kroku wywołujemy rekurencyjnie metodę dla wszystkich punktów po wypłynięciu, zza których jednostka może kontynuować rejs. Wywołanie rekurencyjne następuje dla wartości promienia pomniejszonego o przebytą już drogę. W celu zmniejszenia liczby wywołań, każda rekurencyjnie wywołana funkcja zapamiętuje punkty, dla których została już wywołana, tak by nie wywoływać jej ponownie dla tego samego punktu. Na schemacie poniżej strzałkami zaznaczono miejsca, w których nastąpi rekurencyjne wywołanie metody.

Wyniki działania metody dla wywołań rekurencyjnych należy dodać do ostatecznego rezultatu metody. W ten sposób ze złożenia trójkątów i wycinków kołowych powstaje powierzchnia wewnątrz której znajduje się poszukiwana jednostka. Wynik działania metody naniesiony jest na schemacie poniżej.

Opisany powyżej algorytm w pracy magisterskiej został wzbogacony o dodatkowe dane i wykorzystany do obliczenia prawdopodieństwa położenia jednostki w danym miejscu:

Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C# | MS Visual Studio .net | .cs | .cs | ***** / 3 |
Poprawiony: 14 sierpnia 2012 21:30


