Wpisany przez Tomasz Lubiński,
10 maja 2008 11:00
Załóżmy, że chcemy obliczyć całkę z funkcji f(x) w przedziale <xp; xk>. Definicja całki oznaczonej Riemana, mówi nam, że wartość całki równa jest polu obszaru pod wykresem krzywej w zadanym przedziale całkowania.
Przedstawiona tutaj metoda Monte Carlo polega na wylosowaniu n punktów znajdujących się w obrębie przedziału całkowania i na tej podstawie obliczeniu średniej wartości funkcji w tym przedziale.
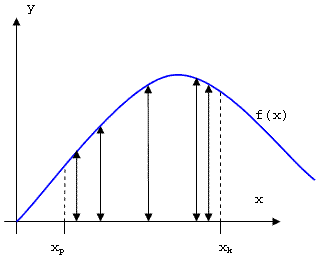
Wartości kolejnych wylosowanych punktów to: x1 = 2.4, x2 = 3.1, x3 = 6, x4 = 9, x5 = 9.5, a wartości funkcji całkowanej w tych punktach to: f(x1) = 3, f(x2) = 3.5, f(x3) = 5, f(x4) = 5.1, f(x5) = 4.4
Najpierw obliczymy wartość średnią: (3 + 3.5 + 5 + 5.1 + 4.4) / 5 = 21 / 5 = 4.2
A następnie pomnożymy tą wartość przez długość przedziału całkowania otrzymując przybliżoną wartość całki: (10 - 2) * 4.2 = 8 * 4.2 = 33.6

f_{sr} = \frac{f(x_1) + f(x_2) + ... + f(x_n)}{n}
A przybliżoną wartość całki mnożąc uzyskaną wartość średnią przez długość całkowanego przedziału:
f_{sr} * |x_k - x_p|
Wraz ze zwiększaniem się liczby punktów pomiarowych n, rozkładają się one coraz bardziej równomiernie w obrębie wyznaczonego przedziału dając coraz dokładniejszy wynik. Z drugiej zaś strony uważać należy by przy dużych ilościach punktów pomiarowych nie przekroczyć zakresu używanych zmiennych podczas dodawania przy obliczaniu wartości średniej. Zabezpieczyć się można przed takim przypadkiem obliczając wartość średnią następująco:
f_{sr} = \frac{f(x_1)}{n} + \frac{f(x_2)}{n} + ... + \frac{f(x_n)}{n}
ale z kolei mamy tutaj problem nakładania się na siebie zaokrągleń z dzielenia przez n.Przykład:
Załóżmy, iż na wykresie powyżej zakres całkowania to: xp = 2, xk = 10Wartości kolejnych wylosowanych punktów to: x1 = 2.4, x2 = 3.1, x3 = 6, x4 = 9, x5 = 9.5, a wartości funkcji całkowanej w tych punktach to: f(x1) = 3, f(x2) = 3.5, f(x3) = 5, f(x4) = 5.1, f(x5) = 4.4
Najpierw obliczymy wartość średnią: (3 + 3.5 + 5 + 5.1 + 4.4) / 5 = 21 / 5 = 4.2
A następnie pomnożymy tą wartość przez długość przedziału całkowania otrzymując przybliżoną wartość całki: (10 - 2) * 4.2 = 8 * 4.2 = 33.6
Przykład w JavaScript:
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C# | MS Visual Studio .net | .cs | .cs | ***** / 1 |
| Tomasz Lubiński | C/C++ | .cpp | .cpp | ***** / 1 | |
| Tomasz Lubiński | Delphi/Pascal | .pas | .pas | ***** / 1 | |
| Tomasz Lubiński | Java | .java | .java | ***** / 1 | |
| Tomasz Lubiński | JavaScript | .js | .js | ***** / 0 |
Poprawiony: 04 października 2012 15:50


