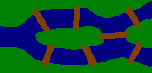Do powstania cyklu Eulera przyczynił się tzw. problem mostów królewieckich. Przez Królewiec (dziś Kaliningrad) przepływała rzeka, w rozwidleniu której znajdowały się 2 wyspy. Na rzece znajdowało się 7 mostów (patrz rys.). Miejscowa ludność co rok urządzała zabawę,która polegała na próbowaniu przebycia wszysktkich mostów dokładnie raz. Problemem tym zajął się Leonhard Euler, szwajcarski matematyk, fizyk i astronom. Udowodnił on, że nie jest to możliwe, powodem tego jest nieparzysta liczba wejść na mosty na wyspach oraz po obu stronach rzeki.
Cyklem Eulera w grafie nazywamy cykl (drogę, która zaczyna się i kończy w tym samym wierzchołku), który zawiera każdą krawędź dokładnie raz.

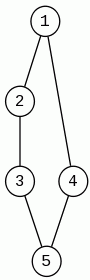
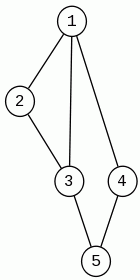
Graf z cyklem Eulera	Graf bez cyklu Eulera

Łańcuchem Eulera w grafie nazywamy drogę, który zawiera każdą krawędź dokładnie raz.
Warunek istnienia cyklu Eulera: po pierwsze graf musi być spójny (musi istnieć droga łącząca każdą parę wierzchołków). Jeżeli graf jest spójny i skierowany to do każdego wierzchołka musi wchodzić i wychodzić tyle samo krawędzi. Jeżeli graf jest spójny i nieskierowany to liczba wychodzących krawędzi z każdego wierzchołka musi być parzysta.

Opis algorytmu