Wpisany przez Michał Knasiecki,
01 sierpnia 2005 19:09
Większość prezentowanych na tej witrynie algorytmów to tzw. algorytmy wielomianowe, tzn. takie, których złożoność czasowa
wynosi O(nk), gdzie n jest rozmiarem danych wejściowych a k pewną stałą. W zależności od wielkości tej stałej, dany algorytm będzie
realizowany szybciej lub wolniej, lecz zawsze jego złożoność jest ograniczona przez pewien wielomian (zob. rzędy wielkości funkcji).
Przykładowo dla algorytmu sortowania przez zliczanie k=1, czyli złożoność wynosi O(n), mówimy, że algorytm ten działa
w czasie linowym. Algorytm sortowania bąbelkowego działa w czasie O(n2), jego złożoność jest więc o wiele większa,
niż złożoność algorytmu sortowania przez zliczanie, oba jednak są ograniczone przez wielomian, czyli są algorytmami wielomianowymi.
Powstaje pytanie: czy wszystkie algorytmy da się rozwiązać w czasie wielomianowym?
Każdy, kto dokładnie zaznajomił się z wszystkimi algorytmami na tej witrynie wie, że tak niestety nie jest. Przykładem może być algorytm wyznaczania cyklu Hamiltona. Rozdzieliliśmy już wyraźnie algorytmy na dwie grupy, teraz opiszemy je trochę formalniej:
Wszystkie problemy decyzyjne, które w co najwyżej wielomianowym czasie są rozwiązywane przez DTM (Deterministyczna Maszyn Turinga) tworzą klasę P (P- ang. polynomial: wielomianowy).
Wszystkie problemy decyzyjne, które w co najwyżej wielomianowym czasie są rozwiązywane przez NDTM (Niedeterministyczna Maszyna Turinga) tworzą klasę NP (NP- ang. nondeterministic polynomial: niedeterministycznie wielomianowy).
Jak dotąd nikomu nie udało się udowodnić, ani zaprzeczyć, że P=NP. Problem ten został sformułowany w roku 1971 i pozostaje otwary do dziś. Większość naukowców uważa jednak, że klasa P i NP nie są sobie równe, chodź podkreślam: nie ma na to dowodu! Przy takim założeniu wykres zależności między klasami przedstawia się następująco:
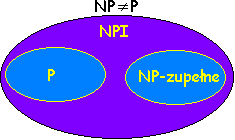
Temat NP-Zupełności jest bardzo obszerny i zawiera całą masę dowodów, ja ograniczyłem się tu tylko do pewnych podstawowych pojęć, których zrozumienia wymagają niektóre algorytmy. Zaciekawionym tym tematem proponuję lekturę Cormena, Leisersona i Rivesta. Opisują onie ten dział informatyki bardzo szczegółowo.
Powstaje pytanie: czy wszystkie algorytmy da się rozwiązać w czasie wielomianowym?
Każdy, kto dokładnie zaznajomił się z wszystkimi algorytmami na tej witrynie wie, że tak niestety nie jest. Przykładem może być algorytm wyznaczania cyklu Hamiltona. Rozdzieliliśmy już wyraźnie algorytmy na dwie grupy, teraz opiszemy je trochę formalniej:
Wszystkie problemy decyzyjne, które w co najwyżej wielomianowym czasie są rozwiązywane przez DTM (Deterministyczna Maszyn Turinga) tworzą klasę P (P- ang. polynomial: wielomianowy).
Wszystkie problemy decyzyjne, które w co najwyżej wielomianowym czasie są rozwiązywane przez NDTM (Niedeterministyczna Maszyna Turinga) tworzą klasę NP (NP- ang. nondeterministic polynomial: niedeterministycznie wielomianowy).
Jak dotąd nikomu nie udało się udowodnić, ani zaprzeczyć, że P=NP. Problem ten został sformułowany w roku 1971 i pozostaje otwary do dziś. Większość naukowców uważa jednak, że klasa P i NP nie są sobie równe, chodź podkreślam: nie ma na to dowodu! Przy takim założeniu wykres zależności między klasami przedstawia się następująco:

Temat NP-Zupełności jest bardzo obszerny i zawiera całą masę dowodów, ja ograniczyłem się tu tylko do pewnych podstawowych pojęć, których zrozumienia wymagają niektóre algorytmy. Zaciekawionym tym tematem proponuję lekturę Cormena, Leisersona i Rivesta. Opisują onie ten dział informatyki bardzo szczegółowo.
Poprawiony: 16 sierpnia 2005 21:25
Komentarze

+2
#
Romek
2014-10-21 11:53
W tekście występuje problem NP, ale w tytule jest NP-zupełny i na rysunku jest NP-zupełne. Jaki jest związek jednego z drugim? Jak się zajrzy do Wikipedii to występuje tam jeszcze NP-trudny. Czy te zbiory problemów są rozłączne? Czy może jakaś inna relacja zachodzi między nimi?
Odpowiedz | Odpowiedz z cytatem | Cytować
+1
#
Murdzek
2015-03-25 10:06
Dzięki przydało sie przy robieniu prezentacji
Odpowiedz | Odpowiedz z cytatem | Cytować
Dodaj komentarz


