Wpisany przez Michał Knasiecki,
13 sierpnia 2005 11:03
Jest to jeden z prostszych algorytmów sortowania.
Sprawdzamy całą tablicę od końca, jeżeli trafimy na parę elementów, w której większy poprzedza mniejszy to zamieniamy je miejscami. Po przejściu całej tablicy znów zaczynamy przeszukiwać tą tablicę od końca. Czynność powtarzamy tak długo aż podczas sprawdzania całej tablicy, nie zajdzie ani jedna zamiana elementów. Realizuje się to najczęściej za pomocą zmiennej logicznej.
Algorytm nosi nazwę bąbelkowego, gdyż najmniejsze liczby "wypływają" z dołu tablicy na jej szczyt, podobnie jak bąbelki powietrza w wodzie.
Oto przykład zastosowania dla nieuporządkowanego ciągu liczb <<2, 4, 1, 3>>.
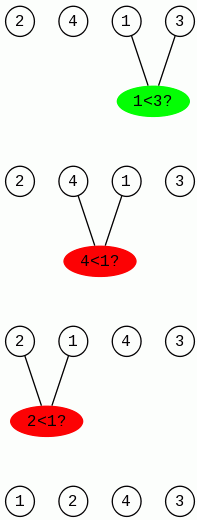
Po pierwszym przejściu wszystkich elementów liczba 1 wypłynęła na wierzch. Rozpoczynamy sprawdzanie tablicy znów od końca.
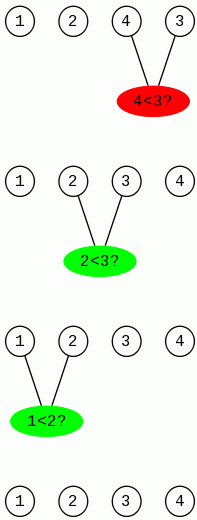
Przy następnym przebiegu nie zajdzie ani jedna zmiana, to znak, że ciąg jest już posortowany.
Z powyższego zdania można wyciągnąć wniosek, że gdy ciąg wejściowy będzie posortowany, to algorytm wykona tylko jeden przebieg. Jest to duża zaleta tego sposobu sortowania, niektóre metody będą sortowały ciąg nawet jeśli będzie on posortowany. Zatem optymistyczna złożoność obliczeniowa tego algorytmu wynosi O(n) - dla posortowanego już ciągu przejdzie on tylko jeden raz po wszystkich elementach.
Z kolei najgorszym zestawem danych dla tego algorytmu jest ciąg posortowany nierosnąco. Tutaj najmniejsze elementy będą "wypływać" po kolei zatem będzie trzeba przejść cały ciąg n razy, a więc pesymistyczna złożoność obliczeniowa wynosi O(n2) i taka też jest jego złożoność w średnim przypadku.
Sprawdzamy całą tablicę od końca, jeżeli trafimy na parę elementów, w której większy poprzedza mniejszy to zamieniamy je miejscami. Po przejściu całej tablicy znów zaczynamy przeszukiwać tą tablicę od końca. Czynność powtarzamy tak długo aż podczas sprawdzania całej tablicy, nie zajdzie ani jedna zamiana elementów. Realizuje się to najczęściej za pomocą zmiennej logicznej.
Algorytm nosi nazwę bąbelkowego, gdyż najmniejsze liczby "wypływają" z dołu tablicy na jej szczyt, podobnie jak bąbelki powietrza w wodzie.
Oto przykład zastosowania dla nieuporządkowanego ciągu liczb <<2, 4, 1, 3>>.


Z powyższego zdania można wyciągnąć wniosek, że gdy ciąg wejściowy będzie posortowany, to algorytm wykona tylko jeden przebieg. Jest to duża zaleta tego sposobu sortowania, niektóre metody będą sortowały ciąg nawet jeśli będzie on posortowany. Zatem optymistyczna złożoność obliczeniowa tego algorytmu wynosi O(n) - dla posortowanego już ciągu przejdzie on tylko jeden raz po wszystkich elementach.
Z kolei najgorszym zestawem danych dla tego algorytmu jest ciąg posortowany nierosnąco. Tutaj najmniejsze elementy będą "wypływać" po kolei zatem będzie trzeba przejść cały ciąg n razy, a więc pesymistyczna złożoność obliczeniowa wynosi O(n2) i taka też jest jego złożoność w średnim przypadku.
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| kris | C# | z użyciem flagi zmiany oraz wypisywaniem kolejnych kroków | .cs | .cs | ***** / 23 |
| Sonquer | C# | bez flagi zmiany | .cs | .cs | ***** / 23 |
| Michał Knasiecki | C/C++ | .cpp | .cpp | ***** / 24 | |
| Marian | C/C++ | C++ streams | .cpp | .cpp | ***** / 13 |
| Krzysztof Sośnierz | C/C++ | C++ templates | .cpp | .cpp | ***** / 9 |
| mariano | C/C++ | C++ | .cpp | .cpp | ***** / 7 |
| Krzysztof Kranc | C/C++ | C++ | .cpp | .cpp | ***** / 2 |
| dawidex44 | C/C++ | C++ - prosty przykład - wszystko w jednej funkcji | .cpp | .cpp | ***** / 103 |
| Mattioo | C/C++ | .cpp | .cpp | ***** / 3 | |
| Piotr Napieralski | C/C++ | Proste i przejrzyste. | .cpp | .cpp | ***** / 2 |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 10 |
| Adam Chrapkowski | Haskell | .hs | .hs | ***** / 0 | |
| Tomasz Lubiński | Java | z użyciem flagi zmiany | .java | .java | ***** / 21 |
| Robert Ziarko | Java | bez flagi zmiany | .java | .java | ***** / 7 |
| Przemysław Pobiedziński | Java | .java | .java | ***** / 17 | |
| Krzysztof | Java | 4 wersje o różnym stopniu optymalizacji | .java | .java | ***** / 8 |
| Maciej Lipiński | JavaScript | funkcja sortująca + test | .js | .js | ***** / 5 |
| Jakub Konieczny | Java_Block | .jbf | .jbf | ***** / 3 | |
| Dominik Goździuk | Perl | .pl | .pl | ***** / 2 | |
| _marass_ | Php | .php | .php | ***** / 17 | |
| Jakub Konieczny | Python | .py | .py | ***** / 18 | |
| Kamil Socha | Python | .py | .py | ***** / 3 |
Poprawiony: 18 listopada 2015 09:34



skorzystam bo baardzo mi sie przyda..hehe...;]
wkońcu skumałam o co w tym chodzi...
poooOzdrówkA.!
nie moze byc warunku ">=" wtedy zamienialby te dwie wartosci. wracal na koniec , dochodzil do nich znowu. zamienial i wracal na koniec. by sie zapletlilo po prostu. algorytm musi to olać
Imho do poprawki bo wprowadza w błąd.