Wpisany przez Tomasz Nędza,
01 sierpnia 2005 23:13
Krzywa Beziera to krzywa wielomianowa trzeciego stopnia, czyli taka która może być definiowana za pomocą trzech wielomianów (odpowiednio dla współrzędnych x, y i z) z pewnym parametrem t. Wielomiany trzeciego stopnia są używane najczęściej, ponieważ wielomiany niższego stopnia są zbyt mało elastyczne, jeśli chodzi o sterowanie kształtem krzywej. Natomiast wielomiany wyższego stopnia wprowadzają niepożądane oscylacje, a ponadto wymagają większej liczby obliczeń. Krzywe trzeciego stopnia są również krzywymi najniższego stopnia, które nie leżą w jednej płaszczyźnie w 3D. Współczynniki wielomianów są tak dobierane, żeby krzywa przebiegała wzdłuż pożądanej ścieżki.
Krzywa ta została opracowana przez Pierre'a Beziera z myślą o wykorzystaniu przy projektowaniu samochodów w firmie Renault.
Krzywa określona jest przez dwa punkty końcowe oraz dwa punkty pośrednie nie należące do krzywej. Krzywa Beziera interpoluje więc oba końcowe punkty i aproksymuje dwa pozostałe.
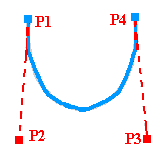
t - parametr z przedziału [0;1] określający, w którym miejscu krzywej znajduje się szukany punkt. Przykładowo dla t=0 otrzymujemy punkt P1, a dla t=1 punkt P4.
Aby otrzymać obraz (współrzędne punktów) całej krzywej należy zmieniać wartość t z odpowiednio małym krokiem. Poniżej znajduje się rysunek krzywej Beziera dla t zwiększanym z krokiem około 0,1.

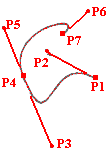
Oznacza to, że wspólny punkt końcowy oraz dwa punkty pośrednie muszą być różne i współliniowe.

P.x=(1-t)^3*P_1.x + 3*(1-t)^2*t*P_2.x + 3*(1-t)*t^2*P_3.x + t^3*P_4.x\\\\
P.y=(1-t)^3*P_1.y + 3*(1-t)^2*t*P_2.y + 3*(1-t)*t^2*P_3.y + t^3*P_4.y\\\\
P.z=(1-t)^3*P_1.z + 3*(1-t)^2*t*P_2.z + 3*(1-t)*t^2*P_3.z + t^3*P_4.z
P.x - wspolrzedna x punktu Pt - parametr z przedziału [0;1] określający, w którym miejscu krzywej znajduje się szukany punkt. Przykładowo dla t=0 otrzymujemy punkt P1, a dla t=1 punkt P4.
Aby otrzymać obraz (współrzędne punktów) całej krzywej należy zmieniać wartość t z odpowiednio małym krokiem. Poniżej znajduje się rysunek krzywej Beziera dla t zwiększanym z krokiem około 0,1.

Oznacza to, że wspólny punkt końcowy oraz dwa punkty pośrednie muszą być różne i współliniowe.

Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Jakub Konieczny | Java_Block | Prosty przykład dla dwóch punktów | .jbf | .jbf | ***** / 5 |
Poprawiony: 01 września 2012 14:22


