Wpisany przez Tomasz Lubiński,
08 sierpnia 2005 21:24
Metoda ta, zwana również metodą Newtona-Raphsona lub metodą stycznych, pozwala obliczyć miejsca zerowe funkcji nieliniowych w przedziałach, musi ona jednak spełniać następujące warunki:
Metoda przebiega następująco: badamy znaki funkcji i drugiej pochodnej na krańcach badanego przedziału <a, b>. Za punkt x(0) wybieramy ten koniec przedziału, w którym funkcja i jej druga pochodna mają równe znaki, a wzór na kolejne punkty wygląda następująco:
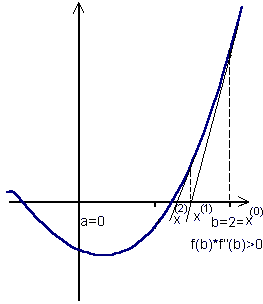
Po pewnej liczbie kroków albo otrzymujemy pierwiastek dokładny albo ciąg przedziałów zbieżny do pierwiastka. Maksymalny błąd i-tego przybliżenia to:
- funkcja f oraz jej pierwsza i druga pochodna są ciągłe w badanym przedziale <a, b>,
- wewnątrz <a, b> znajduje się dokładnie jeden pierwiastek,
- f(a)*f(b) < 0,
- pierwsza i druga pochodna mają stały znak w badanym przedziale <a ,b>.
Metoda przebiega następująco: badamy znaki funkcji i drugiej pochodnej na krańcach badanego przedziału <a, b>. Za punkt x(0) wybieramy ten koniec przedziału, w którym funkcja i jej druga pochodna mają równe znaki, a wzór na kolejne punkty wygląda następująco:
x_i = x_{i-1} - \frac{f(x_{i-1})}{f'(x_{i-1})}
Geometryczną konstrukcję kolejnych przybliżeń pierwiastków obrazuje poniższy wykres (z którego można zresztą powyższe zależności wyznaczyć). Z punktu prowadzimy styczną do krzywej miejsce przecięcia z osią OX tworzy nowy punkt, z którego prowadzimy kolejną styczną, itd...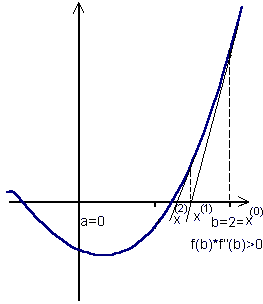
Po pewnej liczbie kroków albo otrzymujemy pierwiastek dokładny albo ciąg przedziałów zbieżny do pierwiastka. Maksymalny błąd i-tego przybliżenia to:
\frac{\max x \in <a,b>|f''(x)|}{2*\min x \in <a,b>|f'(x)|}*\left(\frac{f(x_i)}{f'(x_i)}\right)^2
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C/C++ | .cpp | .cpp | ***** / 12 | |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 3 |
| Tomasz Lubiński | Java | .java | .java | ***** / 8 |
Poprawiony: 26 września 2012 20:19


