Wpisany przez Rafał Pytko,
26 września 2009 12:24
Dla grafów nieskierowanych zostało zdefiniowane pojęcie spójnych składowych, czyli maksymalnych fragmentów grafu, które są spójne (pomiędzy każdymi dwoma wierzchołkami istnieje ścieżka). Do sprawdzania czy graf jest spójny oraz znajdowania jego spójnych składowych wykorzystywany jest algorytm DFS lub BFS.
Odpowiednikiem tej definicji dla grafów skierowanych są silnie spójne składowe. Silnie spójna składowa grafu skierowanego, to taki maksymalny podgraf, w którym istnieje ścieżka (skierowana) pomiędzy każdymi dwoma wierzchołkami tego podgrafu. Maksymalny czyli taki, którego nie możemy już powiększyć tak, aby dalej spełniał nasze założenie. Spójrzmy na poniższy przykład.
Uwaga: Na przykład podgraf złożony z wierzchołków (2,3,4) nie jest silnie spójną składową, gdyż nie jest maksymalnym, który spełnia założenie o istnieniu ścieżek. Maksymalny to (2,3,4,7).
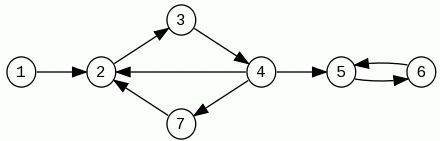
Spójne składowe w naszym przykładzie to:
(1)
(2,3,4,7)
(5,6)
Algorytm:
Aby opisać algorytm wyznaczania silnie spójnych składowych będzie nam potrzebna definicja grafu transponowanego. Graf transponowany jakiegoś grafu powstaje przez zamianę kierunku jego wszystkich krawędzi. Czyli jeśli w naszym oryginalnym grafie występowała krawędź 1 -> 2, to w grafie transponowanym zostanie zamieniona na krawędź 2 -> 1.
Spójrzmy jak wygląda graf transponowany dla grafu z poprzedniego przykładu:
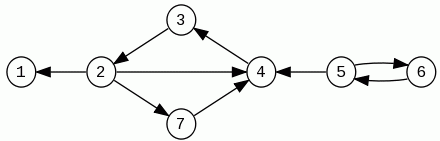
Algorytm wyznaczania silnie spójnych składowych grafu skierowanego:
Spójrzmy na działanie algorytmu dla naszego przykładowego grafu.
Faza 1:
Uruchamiamy algorytm DFS z wierzchołka 1. Idziemy do wierzchołka 2 -> 3 -> 4 -> 5 -> 6 (ustawiając kolejne wierzchołki jako odwiedzone). Z wierzchołka 6 nie możemy już iść do żadnego nieodwiedzonego wierzchołka (5 już był odwiedzony), ustawiamy czas przetworzenia wierzchołka 6 na 1.
Z wierzchołka 5 też nie możemy już nigdzie iść (w 6 już byliśmy) czyli czas przetworzenia ustawiamy na 2.
Z wierzchołka 4 idziemy do 7. Z wierzchołka 7 nie możemy już nigdzie iść (wierzchołek 2 już jest odwiedzony), czyli czas przetworzenia 7-mki to 3.
Teraz już nie możemy nigdzie iść z wierzchołka 4, czyli czas przetworzenia ustawiamy na 4.
Z wierzchołka 3 też już nigdzie nie możemy iść, czas przetworzenia 5.
Tak samo dla wierzchołka 2, czas przetworzenia 6.
Tak samo dla wierzchołka 1, czas przetworzenia 7.
Faza 2:
Będziemy rozpatrywać wierzchołki w kolejności malejących czasów przetworzenia czyli: Wierzchołki nr: 1, 2, 3, 4, 7, 5, 6
W grafie transponowanym startujemy algorytm DFS.
Zaczynamy z wierzchołka 1.
Odwiedzimy tylko wierzchołek nr 1. Jest to nasza pierwsza silnie spójna składowa.
Startujemy z wierzchołka 2.
Odwiedzamy 2, 7, 4, 3. Jest to nasza druga silnie spójna składowa.
Z wierzchołków 3, 4 i 7 nie startujemy, bo już były odwiedzone.
Startujemy z wierzchołka 5.
Odwiedzamy 5 i 6. Jest to kolejna silnie spójna składowa.
Z wierzchołka 6 nie startujemy, bo już był odwiedzony wcześniej.
W ten sposób uzyskaliśmy trzy silnie spójne składowe: (1), (2,3,4,7) oraz (5,6).
Graf silnie spójnych składowych:
Zauważmy, że po obliczeniu silnie spójnych składowych możemy "skompresować" nasz graf. Wierzchołki odpowiadają silnie spójnym składowym. Pomiędzy dwoma silnie spójnymi składowymi jest krawędź, jeśli istniała krawędź pomiędzy dwoma wierzchołkami z tych składowych. Taki graf nie zawiera cykli, gdyż byłoby to sprzeczne z tym, że silnie spójne składowe są maksymalne.
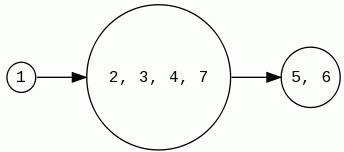
Zastosowanie:
Złożoność czasowa tego algorytmu jest liniowa względem liczby wierzchołków i krawędzi, jest to dwukrotne wywołanie algorytmu przeszukiwania w głąb. Jest to zatem szybki algorytm.
Czasami zachodzi potrzeba przekształcenia naszego grafu w graf bez cykli i dalszego operowania na takim grafie, wówczas możemy zastosować powyższy algorytm.
Mając daną sieć dróg pomiędzy miastami (drogi jednokierunkowe) chcemy sprawdzić czy z każdego miasta da się dojechać do każdego innego. Wówczas wystarczy sprawdzić czy nasz graf jest jedną silnie spójną składową. Wyznaczanie silnie spójnych składowych grafu jest również wykorzystywane w algorytmie spełnialności formuł dwuargumentowych (2SAT).
Odpowiednikiem tej definicji dla grafów skierowanych są silnie spójne składowe. Silnie spójna składowa grafu skierowanego, to taki maksymalny podgraf, w którym istnieje ścieżka (skierowana) pomiędzy każdymi dwoma wierzchołkami tego podgrafu. Maksymalny czyli taki, którego nie możemy już powiększyć tak, aby dalej spełniał nasze założenie. Spójrzmy na poniższy przykład.
Przykład:
Uwaga: Na przykład podgraf złożony z wierzchołków (2,3,4) nie jest silnie spójną składową, gdyż nie jest maksymalnym, który spełnia założenie o istnieniu ścieżek. Maksymalny to (2,3,4,7).

Spójne składowe w naszym przykładzie to:
(1)
(2,3,4,7)
(5,6)
Algorytm:
Aby opisać algorytm wyznaczania silnie spójnych składowych będzie nam potrzebna definicja grafu transponowanego. Graf transponowany jakiegoś grafu powstaje przez zamianę kierunku jego wszystkich krawędzi. Czyli jeśli w naszym oryginalnym grafie występowała krawędź 1 -> 2, to w grafie transponowanym zostanie zamieniona na krawędź 2 -> 1.
Spójrzmy jak wygląda graf transponowany dla grafu z poprzedniego przykładu:

Algorytm wyznaczania silnie spójnych składowych grafu skierowanego:
- Oblicz czasy przetworzenia (post-order) wierzchołków algorytmem przeszukiwania w głąb (DFS).
- Wywołujemy algorytm DFS dla grafu transponowanego w kolejności malejących czasów przetworzenia wierzchołków. Wszystkie wierzchołki w jednym drzewie przeszukiwania w głąb należą do jednej silnie spójnej składowej.
Przykład:
Spójrzmy na działanie algorytmu dla naszego przykładowego grafu.
Faza 1:
Uruchamiamy algorytm DFS z wierzchołka 1. Idziemy do wierzchołka 2 -> 3 -> 4 -> 5 -> 6 (ustawiając kolejne wierzchołki jako odwiedzone). Z wierzchołka 6 nie możemy już iść do żadnego nieodwiedzonego wierzchołka (5 już był odwiedzony), ustawiamy czas przetworzenia wierzchołka 6 na 1.
Z wierzchołka 5 też nie możemy już nigdzie iść (w 6 już byliśmy) czyli czas przetworzenia ustawiamy na 2.
Z wierzchołka 4 idziemy do 7. Z wierzchołka 7 nie możemy już nigdzie iść (wierzchołek 2 już jest odwiedzony), czyli czas przetworzenia 7-mki to 3.
Teraz już nie możemy nigdzie iść z wierzchołka 4, czyli czas przetworzenia ustawiamy na 4.
Z wierzchołka 3 też już nigdzie nie możemy iść, czas przetworzenia 5.
Tak samo dla wierzchołka 2, czas przetworzenia 6.
Tak samo dla wierzchołka 1, czas przetworzenia 7.
Faza 2:
Będziemy rozpatrywać wierzchołki w kolejności malejących czasów przetworzenia czyli: Wierzchołki nr: 1, 2, 3, 4, 7, 5, 6
W grafie transponowanym startujemy algorytm DFS.
Zaczynamy z wierzchołka 1.
Odwiedzimy tylko wierzchołek nr 1. Jest to nasza pierwsza silnie spójna składowa.
Startujemy z wierzchołka 2.
Odwiedzamy 2, 7, 4, 3. Jest to nasza druga silnie spójna składowa.
Z wierzchołków 3, 4 i 7 nie startujemy, bo już były odwiedzone.
Startujemy z wierzchołka 5.
Odwiedzamy 5 i 6. Jest to kolejna silnie spójna składowa.
Z wierzchołka 6 nie startujemy, bo już był odwiedzony wcześniej.
W ten sposób uzyskaliśmy trzy silnie spójne składowe: (1), (2,3,4,7) oraz (5,6).
Graf silnie spójnych składowych:
Zauważmy, że po obliczeniu silnie spójnych składowych możemy "skompresować" nasz graf. Wierzchołki odpowiadają silnie spójnym składowym. Pomiędzy dwoma silnie spójnymi składowymi jest krawędź, jeśli istniała krawędź pomiędzy dwoma wierzchołkami z tych składowych. Taki graf nie zawiera cykli, gdyż byłoby to sprzeczne z tym, że silnie spójne składowe są maksymalne.

Zastosowanie:
Złożoność czasowa tego algorytmu jest liniowa względem liczby wierzchołków i krawędzi, jest to dwukrotne wywołanie algorytmu przeszukiwania w głąb. Jest to zatem szybki algorytm.
Czasami zachodzi potrzeba przekształcenia naszego grafu w graf bez cykli i dalszego operowania na takim grafie, wówczas możemy zastosować powyższy algorytm.
Mając daną sieć dróg pomiędzy miastami (drogi jednokierunkowe) chcemy sprawdzić czy z każdego miasta da się dojechać do każdego innego. Wówczas wystarczy sprawdzić czy nasz graf jest jedną silnie spójną składową. Wyznaczanie silnie spójnych składowych grafu jest również wykorzystywane w algorytmie spełnialności formuł dwuargumentowych (2SAT).
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Rafał Pytko | C/C++ | .cpp | .cpp | ***** / 15 | |
| Emil Hotkowski | C/C++ | SSS na vectorach | .cpp | .cpp | ***** / 6 |
Poprawiony: 15 stycznia 2012 20:10



Wypadałoby jednak wspomnieć że jest to algorytm Kosaraju. Właściwie to szukając Kosaraju przez polskie Google nic się nie dowiemy, dopiero angielska Wikipedia przybliża sprawę -
To trochę utrudnia poszukiwania. Ale jeśli będziemy go szukać ze względu na zastosowanie to faktycznie łatwo znaleźć