Wpisany przez Michał Knasiecki,
03 sierpnia 2005 22:41
Zrozumienie tego algorytmu wymaga zaznajomienia się z tematami: Wstęp do geometrii obliczeniowej, Przynależność punktu do odcinka, Przecinanie się odcinków.
Istnieje bardzo łatwy sposób stwierdzenia, czy punkt należy do prostokąta. Wystarczy zauważyć, że rzuty prostokątne tego punktu na osie OX i OY wpadają do rzutów prostokątnych boków tego prostokąta. Co jednak zrobić, gdy musimy sprawdzić, czy punkt należy do wielokąta o liczbie boków większej niż 4? Wielokąt ten można podzielić na trójkąty i sprawdzać, czy nasz punkt należy do jednego z nich. Można jednak skorzystać z pewnej własności, którą dostarcza nam geometria obliczeniowa, a mianowicie: dany jest wielokąt W oraz punkt p. Z punktu p kreślimy w dowolnym kierunku półprostą l i liczymy ile razy półprosta przecina boki wielokąta W. Jeżeli półprosta przecina wielokąt nieparzystą liczbę razy to punkt p należy do wielokąta W, w przeciwnym razie punkt nie należy do wielokąta.
 Oto przykład:
Oto przykład:
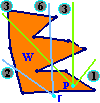
Przeanalizujmy sytuację przedstawioną na rysunku.
Fioletowe półproste przecinają boki nieparzystą liczbę razy, na podstawie powyższego twierdzenia można stwierdzić, że punkt p należy do W.
Półproste koloru brązowego przecinają boki W parzystą liczbę razy, punkt r nie należy więc do wielokąta.
W przykładzie tym wyprowadziłem kilka półprostych, lecz wystarczy oczywiście tylko jedna. Na powyższym rysunku żadna z półprostych nie przecina brzegu wielokąta w wierzchołkach. Należy ustalić liczbę przecięć, którą będziemy brali pod uwagę gdy do naszej półprostej będzie należał jeden z wierzchołków wielokąta. Można wyróżnić dwa takie przypadki:
Sytuacja 1: w prostej l zawiera się jeden z boków wielokąta, powiedzmy b. Dwa boki sąsiadujące z b nazwijmy c i d. Końce tych boków nie należące do b nazwijmy x oraz y. Przyjmiemy, że półprosta przecięła boki b, c i d w jednym punkcie, jeżeli punkty x i y leżą po przeciwnych stronach półprostej l (rys. b). Jeśli punkty te leżą po tej samej stronie (rys. a) przyjmiemy, że półprosta nie przeciną powyższych boków.
Sytuacja 2: wierzchołek v wielokąta W należy do prostej l, która nie zawiera żadnego z boków z nim sąsiadujących, nazwijmy te boki b i c, niech x i y będą końcami tych boków. Jeżeli x i y leżą po przeciwnych stronach półprostej (rys. c) to przyjmujemy, że półprosta przecina boki b i c w jednym punkcie, w przeciwnym wypadku (rys. d) nie przecina ich wcale.
Takie założenia są słuszne. Można bowiem zauważyć, że obracając naszą półprostą l o pewien niewielki kąt zgodnie z kierunkiem ruchu wskazówek zegara otrzymamy dokładnie taką liczbę przecięć, jaką założyliśmy.
Sytuacja 3: osobną klasą przypadków, którą również powinniśmy wziąć pod uwagę, jest przynależność punktu do krawędzi wielokąta. Takie sprawdzenie powinniśmy wykonywać równocześnie ze zliczaniem przecięć. Jeżeli punkt należy, do którejś z krawędzi, to jeżeli zakładamy, że krawędzie należą również do wielokąta to również zaliczymy go do punktów należących do wielokąta.
Poznaliśmy już algorytmy sprawdzający, czy punkt należy do odcinka oraz czy dwa punkty leżą po przeciwnych stronach odcinka. W tym problemie mamy jednak do czynienia z półprostą. Należy więc umieścić na tej półprostej punkt - otrzymamy wtedy odcinek. Ważne jest jednak, by punkt ten leżał poza naszym wielokątem. Jak to zrobić? Sposób jest bardzo prosty. Umówmy się, że nasza półprosta będzie zawsze równoległa do osi OX oraz "zwrócona" w prawą stronę, czyli grot wektora zaczepionego w początku półprostej będzie się znajdował po prawej stronie tego początku. Możemy to założenie poczynić, gdyż do rozwiązania naszego problemu może posłużyć dowolna półprosta. Obierając nasz punkt na półprostej, który ma się znaleźć poza wielokątem mamy już jego jedną współrzędną: rzędna jest taka sama jak pierwszego punktu (półprosta jest równoległa do osi OX). Aby wyznaczyć jej odciętą wystarczy podczas wczytywania współrzędnych wierzchołków wielokąta zapamiętać odciętą punktu najdalej wysuniętego w prawo. Następnie do tej liczby dodajemy 1 i otrzymujemy naszą odciętą. Mamy pewność, że znajduje się poza wielokątem, gdyż jest o jedną jednostkę za najdalej wysuniętym wierzchołkiem. Dla pełnej jasności umieszczam rysunek: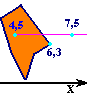
Istnieje bardzo łatwy sposób stwierdzenia, czy punkt należy do prostokąta. Wystarczy zauważyć, że rzuty prostokątne tego punktu na osie OX i OY wpadają do rzutów prostokątnych boków tego prostokąta. Co jednak zrobić, gdy musimy sprawdzić, czy punkt należy do wielokąta o liczbie boków większej niż 4? Wielokąt ten można podzielić na trójkąty i sprawdzać, czy nasz punkt należy do jednego z nich. Można jednak skorzystać z pewnej własności, którą dostarcza nam geometria obliczeniowa, a mianowicie: dany jest wielokąt W oraz punkt p. Z punktu p kreślimy w dowolnym kierunku półprostą l i liczymy ile razy półprosta przecina boki wielokąta W. Jeżeli półprosta przecina wielokąt nieparzystą liczbę razy to punkt p należy do wielokąta W, w przeciwnym razie punkt nie należy do wielokąta.
 Oto przykład:
Oto przykład:Przeanalizujmy sytuację przedstawioną na rysunku.
Fioletowe półproste przecinają boki nieparzystą liczbę razy, na podstawie powyższego twierdzenia można stwierdzić, że punkt p należy do W.
Półproste koloru brązowego przecinają boki W parzystą liczbę razy, punkt r nie należy więc do wielokąta.
W przykładzie tym wyprowadziłem kilka półprostych, lecz wystarczy oczywiście tylko jedna. Na powyższym rysunku żadna z półprostych nie przecina brzegu wielokąta w wierzchołkach. Należy ustalić liczbę przecięć, którą będziemy brali pod uwagę gdy do naszej półprostej będzie należał jeden z wierzchołków wielokąta. Można wyróżnić dwa takie przypadki:
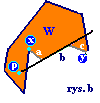
Sytuacja 1: w prostej l zawiera się jeden z boków wielokąta, powiedzmy b. Dwa boki sąsiadujące z b nazwijmy c i d. Końce tych boków nie należące do b nazwijmy x oraz y. Przyjmiemy, że półprosta przecięła boki b, c i d w jednym punkcie, jeżeli punkty x i y leżą po przeciwnych stronach półprostej l (rys. b). Jeśli punkty te leżą po tej samej stronie (rys. a) przyjmiemy, że półprosta nie przeciną powyższych boków.
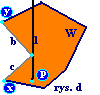
Sytuacja 2: wierzchołek v wielokąta W należy do prostej l, która nie zawiera żadnego z boków z nim sąsiadujących, nazwijmy te boki b i c, niech x i y będą końcami tych boków. Jeżeli x i y leżą po przeciwnych stronach półprostej (rys. c) to przyjmujemy, że półprosta przecina boki b i c w jednym punkcie, w przeciwnym wypadku (rys. d) nie przecina ich wcale.
 |
 |
 |
 |
Liczba przecięć: 1 (1+0) |
Liczba przecięć: 3 (2+1) |
Liczba przecięć: 1 (1) |
Liczba przecięć: 1 (1+0) |
Takie założenia są słuszne. Można bowiem zauważyć, że obracając naszą półprostą l o pewien niewielki kąt zgodnie z kierunkiem ruchu wskazówek zegara otrzymamy dokładnie taką liczbę przecięć, jaką założyliśmy.
Sytuacja 3: osobną klasą przypadków, którą również powinniśmy wziąć pod uwagę, jest przynależność punktu do krawędzi wielokąta. Takie sprawdzenie powinniśmy wykonywać równocześnie ze zliczaniem przecięć. Jeżeli punkt należy, do którejś z krawędzi, to jeżeli zakładamy, że krawędzie należą również do wielokąta to również zaliczymy go do punktów należących do wielokąta.
Poznaliśmy już algorytmy sprawdzający, czy punkt należy do odcinka oraz czy dwa punkty leżą po przeciwnych stronach odcinka. W tym problemie mamy jednak do czynienia z półprostą. Należy więc umieścić na tej półprostej punkt - otrzymamy wtedy odcinek. Ważne jest jednak, by punkt ten leżał poza naszym wielokątem. Jak to zrobić? Sposób jest bardzo prosty. Umówmy się, że nasza półprosta będzie zawsze równoległa do osi OX oraz "zwrócona" w prawą stronę, czyli grot wektora zaczepionego w początku półprostej będzie się znajdował po prawej stronie tego początku. Możemy to założenie poczynić, gdyż do rozwiązania naszego problemu może posłużyć dowolna półprosta. Obierając nasz punkt na półprostej, który ma się znaleźć poza wielokątem mamy już jego jedną współrzędną: rzędna jest taka sama jak pierwszego punktu (półprosta jest równoległa do osi OX). Aby wyznaczyć jej odciętą wystarczy podczas wczytywania współrzędnych wierzchołków wielokąta zapamiętać odciętą punktu najdalej wysuniętego w prawo. Następnie do tej liczby dodajemy 1 i otrzymujemy naszą odciętą. Mamy pewność, że znajduje się poza wielokątem, gdyż jest o jedną jednostkę za najdalej wysuniętym wierzchołkiem. Dla pełnej jasności umieszczam rysunek:

Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | Ada | .ada | .ada | ***** / 1 | |
| Michał Knasiecki | C/C++ | .cpp | .cpp | ***** / 7 | |
| Michał Knasiecki | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 1 |
| Tomasz Lubiński | Java | .java | .java | ***** / 1 |
Poprawiony: 20 czerwca 2011 21:35



Na pewno program w Pascalu (ale chyba działają tak samo) - weźmy prosty, wcale nie złośliwy przypadek, trójkąt:
250,50
350,250
150,200
oraz punkt (50,50) W programie użyta jest linia od tego punktu do Max_x+1 czyli 351. r=(351, 50). Co się okazuje? W pierwszym wołaniu funkcji przecinanie() idziemy do ostatniego miejsca "if przynaleznosc(p ,r,a) then" i tam korzystamy z tmp, kóre nie jest zainicjowane. Rozumiem, że tmp jest globalne, w jednym wołaniu inicjowane, a w następnym wykorzystywane. Ale co gdy korzystamy z tmp już w pierwszym wywołaniu funkcji. Jak patrzyłem, na inne implementacje, są takie same, różnią się tylko językiem programowania. Jest źle dla wszystkich punktów z przedziału x=(-nieskończoność, 250), y=50; czyli linia przed wierzchołkiem