Wpisany przez Michał Knasiecki,
26 lipca 2005 23:08
Ciąg Fibonacciego wyraża się rekurencyjnym wzorem: f(n)=f(n-2)+f(n-1), gdy f(1)=1 oraz f(2)=1.
Łatwo obliczyć, że:
f(3)=f(1)+f(2)=1+1=2
f(4)=f(2)+f(3)=1+2=3
f(5)=f(3)+f(4)=2+3=5
Rekurencyjne obliczanie n-tego wyrazu ciągu Fibonacciego może być opisane następującym schematem blokowym:
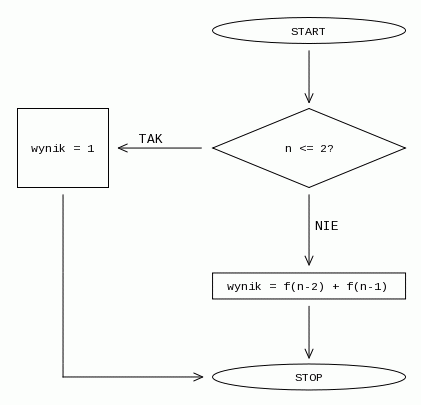
Rekurencyjne obliczanie wartości zajmuje O(2n) czasu i dla bardzo dużych wartości n jest niepraktyczne. O wiele szybciej - w czasie O(log(n)) można obliczyć n-ty wyraz ciągu Fibonacciego używając szybką rekurencję modularną.
Łatwo obliczyć, że:
f(3)=f(1)+f(2)=1+1=2
f(4)=f(2)+f(3)=1+2=3
f(5)=f(3)+f(4)=2+3=5
Rekurencyjne obliczanie n-tego wyrazu ciągu Fibonacciego może być opisane następującym schematem blokowym:

Rekurencyjne obliczanie wartości zajmuje O(2n) czasu i dla bardzo dużych wartości n jest niepraktyczne. O wiele szybciej - w czasie O(log(n)) można obliczyć n-ty wyraz ciągu Fibonacciego używając szybką rekurencję modularną.
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | Ada | .ada | .ada | ***** / 7 | |
| Tomasz Lubiński | C# | MS Visual Studio .net | .cs | .cs | ***** / 15 |
| Michał Knasiecki | C/C++ | .cpp | .cpp | ***** / 20 | |
| Marian | C/C++ | C++ | .cpp | .cpp | ***** / 26 |
| _marass_ | C/C++ | wersja iteracyjna | .cpp | .cpp | ***** / 42 |
| Bartosz Bednarczyk | C/C++ | C++ wersja iteracyjna dla dużych liczb | .cpp | .cpp | ***** / 7 |
| Krzysztof Kozłowski | C/C++ | bez rekurencji, bez iteracji - wzór ogólny | .cpp | .cpp | ***** / 6 |
| Michał Knasiecki | Delphi/Pascal | Borland Delphi | .pas | .pas | ***** / 7 |
| Adam Chrapkowski | Haskell | .hs | .hs | ***** / 1 | |
| Tomasz Lubiński | Java | .java | .java | ***** / 35 | |
| Jakub Konieczny | Java_Block | 3 metody (w zakładkach) | .jbf | .jbf | ***** / 2 |
| _marass_ | Php | wersja iteracyjna | .php | .php | ***** / 6 |
| _marass_ | Php | wersja rekurencyjna | .php | .php | ***** / 5 |
| monika | Python | wersja z użyciem list | .py | .py | ***** / 17 |
Poprawiony: 23 kwietnia 2012 09:06



Ten schemat jest poprawny bo dla 0 wartosc wynosi 1
Po pierwsze, 0-owa liczba Fibonacciego wynosi 0.
pl.wikipedia.org/wiki/Ciąg_Fibonaccie go
Po drugie, czasami przyjmuje się że ciąg Fib. zaczyna się od 1, 1, 2, 3, 5... i indeksuje się go od jedynki.
Czyli:
fib(0) nie istnieje
fib(1) = 1
fib(2) = 1
...
Zatem jeżeli przyjmiemy powyższą definicję ciągu Fib. to schemat jest prawidłowy.
Po trzecie, myślę że schemat powinien być poprawiony tak aby dla 0 i wszystkich niepoprawnych indeksów (np. -17) zwracał 0.
fib(0)=0
fib(1)=1
fib(n)=
: fib(n-1)+fib(n-2) dla n>=2
: fib(n+1)-fib(n+2) dla n
fib(n) =
:0, dla n = 0
:1, dla n = 1
:fib(n-1) + fib(n-2), dla n >= 2
:fib(n+2) - fib(n+1), dla n < 0