Wpisany przez Tomasz Lubiński,
22 lipca 2009 14:44
Podobnie jak w przypadku innych fraktali również dla Płonącego Statku definiuje się zbiory wyższych rzędów. Zbiór o jeden stopień wyższy od Płonącego Statku nazywa się Drapieżny Ptak (ang. Bird of prey). Kolejne, wyższe rzędy nie mają nadanych nazw. Proces generowania przybliżeń takich zbiorów przebiega identycznie jak w przypadku zbioru Płonącego Statku zmienia się jedynie stopień potęgi użytej we wzorze na ciąg.
Poniżej znajdują się definicje zbiorów wraz z ich reprezentacją graficzną (do kolorowania użyto skali logarytmicznej):
Przypomnijmy jeszcze działania na liczbach zespolonych jakie będziemy potrzebować podczas obliczeń. Liczba zespolona z składa się z częsci rzeczywistej zr oraz częsci urojonej zi, czyli
Poniżej znajdują się definicje zbiorów wraz z ich reprezentacją graficzną (do kolorowania użyto skali logarytmicznej):
- Płonący statek
z_0 = 0\\\\ z_{n+1} = ( | \Re(z_n) | + i | \Im(z_n) | )^2 + p
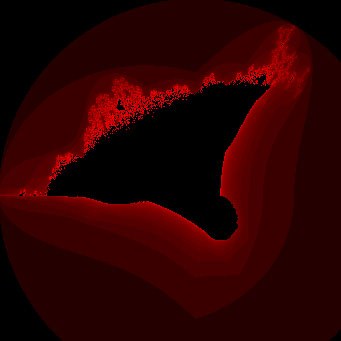
- Drapieżny Ptak
z_0 = 0\\\\ z_{n+1} = ( | \Re(z_n) | + i | \Im(z_n) | )^3 + p

- Quadratur
z_0 = 0\\\\ z_{n+1} = ( | \Re(z_n) | + i | \Im(z_n) | )^4 + p

- Penta
z_0 = 0\\\\ z_{n+1} = ( | \Re(z_n) | + i | \Im(z_n) | )^5 + p

- Hexa
z_0 = 0\\\\ z_{n+1} = ( | \Re(z_n) | + i | \Im(z_n) | )^6 + p

- Hepta
z_0 = 0\\\\ z_{n+1} = ( | \Re(z_n) | + i | \Im(z_n) | )^7 + p

- ...
Przypomnijmy jeszcze działania na liczbach zespolonych jakie będziemy potrzebować podczas obliczeń. Liczba zespolona z składa się z częsci rzeczywistej zr oraz częsci urojonej zi, czyli
z = z_{r} + iz_{i}
Mnożenie definiujemy następująco:
a * b = (a_r*b_r - a_i*b_i) + i(a_r*b_i + a_i*b_r)
Dodawanie definiujemy następująco:
a + b = (a_r + b_r) + i(a_i + b_i)
Moduł z liczby zespolonej definiujemy następująco:
|z|=\sqrt{z_{r}^{2}+z_{i}^{2}}
dlatego też w praktyce warunek |z| < 2 zastępuje się równoważną nierównością
z_{r}^{2}+z_{i}^{2} < 4
Pozbywamy się tutaj czasochłonnego obliczania pierwiastka kwadratowego.Przykład w JavaScript:
Zaznaczając obszar uzyskasz jego powiększony obraz. Kliknięcie prawym klawiszem (bądź dotknięcie dwoma palcami na urządzeniach z ekranem dotykowym) spowoduje powtórne pokazanie całego zbioru.
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C# | MS Visual Studio .net | .cs | .cs | ***** / 1 |
| Tomasz Lubiński | C/C++ | Borland Builder 6 | .cpp | .cpp | ***** / 1 |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 1 |
| Tomasz Lubiński | JavaScript | Firefox 3.0+, Safari 3.0+, Chrome 3.0+, Opera 9.5+, IE 9.0+ | .js | .js | ***** / 0 |
Poprawiony: 27 sierpnia 2012 18:41


