Wpisany przez Tomasz Lubiński,
26 lipca 2011 11:23
IFS czyli system funkcji iterowanych (ang.iterated function system), to zbiór funkcji za pomocą, których konstruuje się fraktale. IFS zostały opisane przez John'a Hutchinson'a w 1981 natomiast spopularyzował je Micheal Barnsley. Formalnie system funkcji iterowanych zapisać można jako zbiór n funkcji przekształcający zbiór S:
Nie dla wszystkich IFS, prawdopodobieństwo wylosowania każdej z funkcji powinno być takie samo, dlatego oprócz zbioru funkcji definiuje się również prawdopodobieństwo pi z jakim dana funkcja powinna zostać wylosowana. Oczywiście suma tych prawdopodobieństw musi wynosić p1 + p2 + ... pn = 1
Obrazy powyżej są czarno-białe. Na czarno zaznaczone są punkty, po których przeszliśmy w trakcie obliczeń, na biało natomiast obszary, których nie osiągnięto.
Dużo lepsze efekty daje zliczanie liczby wystąpień danego punktu podczas obliczeń. Dopiero w kolejnym kroku, punkt zaznaczany jest przy pomocy zmiany jego jasności - im punkt wystąpił więcej razy, tym jest ciemniejszy. Najlepiej do zmiany jasności zastosować skalę logarytmiczną.
S = f_1(S)\\
S = f_2(S)\\
...\\
S = f_n(S)\\
W tym artykule zajmiemy się przypadkiem, gdzie zbiór S będzie reprezentował płaszczyznę dwuwymiarową (opisaną przez współrzędne x oraz y), a funkcje będą przekształceniami afinicznymi tej płaszczyzny, czyli pojedyncza funkcja f(xn; yn) będzie dokonywać następującego przekształcenia:
x_{n+1} = ax_n + by_n + e\\
y_{n+1} = cx_n + dy_n + f
Sposób generowania fraktala z takiego zbioru funkcji przedstawił Barnsley, pod nazwą "gra chaos" (and. chaos game). Przebiega on następująco: dla aktualnego punktu (x; y) wybieramy losowo funkcję ze zbioru i wykonujemy przekształcenie otrzymując nowy punkt. Zaznaczamy punkt na płaszczyźnie następnie znów losujemy funkcję i dokonujemy kolejnego przekształcenia, proces ten powtarzamy określoną liczbę razy (im więcej punktów przetworzymy tym dokładniejszy obraz fraktala otrzymamy). Początkową wartość punktu wybieramy losowo, bądź zaczynamy od punktu (0; 0). Zbiór punktów obliczonych w trakcie tego procesu nazywamy atraktorem danego IFS - jest to atraktor chaotyczny (dziwny atraktor) czyli fraktal.Nie dla wszystkich IFS, prawdopodobieństwo wylosowania każdej z funkcji powinno być takie samo, dlatego oprócz zbioru funkcji definiuje się również prawdopodobieństwo pi z jakim dana funkcja powinna zostać wylosowana. Oczywiście suma tych prawdopodobieństw musi wynosić p1 + p2 + ... pn = 1
| Trójkąt sierpińskiego | ||
 | f1(0.5x + 0.0y - 0.5; 0.0x + 0.5y + 0.5) f2(0.5x + 0.0y - 0.5; 0.0x + 0.5y - 0.5) f3(0.5x + 0.0y + 0.5; 0.0x + 0.5y - 0.5) |
p1 = 0.3333 p2 = 0.3333 p3 = 0.3334 |
| Spirala | ||
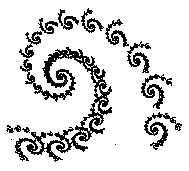 | f1(0.787879x - 0.424242y + 1.758647; 0.242424x + 0.859848y + 1.408065) f2(-0.121212x + 0.257576y - 6.721654; 0.151515x + 0.053030y + 1.377236) f3(0.181818x - 0.136364y + 6.086107; 0.090909x + 0.181818y + 1.568035) |
p1 = 0.895652 p2 = 0.052174 p3 = 0.052174 |
| Smok | ||
 | f1(0.824074x + 0.281428y - 1.882290; -0.212346x + 0.864198y - 0.110607) f2(0.088272x + 0.520988y + 0.785360; -0.463889x - 0.377778y + 8.095795) |
p1 = 0.787473 p2 = 0.212527 |
| Paproć Barnsley'a | ||
 | f1(0.0x + 0.0y + 0.0, 0.0x + 0.16y + 0.0) f2(0.85x + 0.04y + 0.0; -0.04x + 0.85y + 1.6) f3(0.2x - 0.26y + 0.0; 0.23x + 0.22y + 1.6) f4(-0.15x + 0.28y + 0.0; 0.26x + 0.24y + 0.44) |
p1 = 0.01 p2 = 0.85 p3 = 0.07 p4 = 0.07 |
| Liść klonu | ||
 | f1(0.14x + 0.01y - 1.31; 0.0x + 0.51y + 0.1) f2(0.43x + 0.52y + 1.49; -0.45x + 0.5y - 0.75) f3(0.45x - 0.49y - 1.62; 0.47x + 0.47y - 0.74) f4(0.49x + 0.0y + 0.02; 0.0x + 0.51y + 1.62) |
p1 = 0.1 p2 = 0.35 p3 = 0.35 p4 = 0.2 |
| Drzewo | ||
 | f1(0.05x + 0.0y - 0.06; 0.0x + 0.4y - 0.47) f2(-0.05x + 0.0y - 0.06; 0.0x - 0.4y - 0.47) f3(0.03x - 0.14y - 0.16; 0.0x + 0.26y -0.01) f4(-0.03x + 0.14y - 0.16; 0.0x - 0.26y -0.01) f5(0.56x + 0.44y + 0.3; -0.37x + 0.51y + 0.15) f6(0.19x + 0.07y - 0.2; -0.1x + 0.15y + 0.28) f7(-0.33x - 0.34y - 0.54; -0.33x + 0.34y + 0.39) |
p1 = 0.142 p2 = 0.142 p3 = 0.142 p4 = 0.142 p5 = 0.142 p6 = 0.142 p7 = 0.142 |
Obrazy powyżej są czarno-białe. Na czarno zaznaczone są punkty, po których przeszliśmy w trakcie obliczeń, na biało natomiast obszary, których nie osiągnięto.
Dużo lepsze efekty daje zliczanie liczby wystąpień danego punktu podczas obliczeń. Dopiero w kolejnym kroku, punkt zaznaczany jest przy pomocy zmiany jego jasności - im punkt wystąpił więcej razy, tym jest ciemniejszy. Najlepiej do zmiany jasności zastosować skalę logarytmiczną.
Przykład w JavaScript:
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Tomasz Lubiński | C/C++ | Borland Builder 6 | .cpp | .cpp | ***** / 7 |
| Tomasz Lubiński | Delphi/Pascal | Borland Delphi 5 | .pas | .pas | ***** / 1 |
| Tomasz Lubiński | JavaScript | Firefox 3.0+, Safari 3.0+, Chrome 3.0+, Opera 9.5+, IE 9.0+ | .js | .js | ***** / 3 |
| Krzysztof Bruszewski | R | .r | .r | ***** / 4 |
Poprawiony: 27 sierpnia 2012 20:41


