Wpisany przez Andrzej Borucki,
16 sierpnia 2005 19:18
Kopiec inaczej zwany stogiem jest szczególnym przypadkiem drzewa binarnego, które spełnia tzw.warunek kopca tzn. każdy następnik jest niewiększy od swego poprzednika. Z warunku tego wynikają szczególne własności kopca:
Kopiec zupełny – to kopiec będący zupełnym drzewem binarnym. Drzewo binarne jest zupełne wtedy gdy wszystkie poziomy z wyjątkiem ostatniego są całkowicie zapełnione a na ostatnim liście są spójnie ułożone od strony lewej do prawej.
Na poziomie i z wyjątkiem ostatniego jest 2i węzłów
Wysokość takiego kopca jest logarytmiczna względem jego wielkości.
Kopiec zupełny można wygodnie reprezentować w tablicy o indeksie rozpoczynającym się od 1. Następniki węzła k mają numery 2k oraz 2k+1 a poprzednik węzła k ma wartość k/2 (dzielenie bez reszty - np. dla 7 rodzic ma numer 7/2 = 3).
Szczególne własności kopców zostały wykorzystane do stworzenia algorytmy do sortowania zwanego HeapSort
Kopiec pozwala również w wydajny sposób zaimplementować kolejkę priorytetową, gdzie dokładamy do niej różne elementy a wyjmujemy zawsze element największy.
Operacja wstawiania – insert
Operacja usuwania - delete max
Operacja wstawiania elementu do stosu insert:
Wstawiamy element w pierwsze wolne miejsce ostatniego poziomu, a następnie jeżeli wstawiony element jest większy od rodzica, zamieniamy go miejscami. Następnie po zamianie znów sprawdzamy, czy element jest większy od nowego rodzica. Jeżeli tak to znów zamieniamy do miejscami. Operację sprawdzania i zamieniania miejscami powtarzamy tak długo, aż w końcu rodzic będzie większy od wstawionego elementu bądź dojdziemy do korzenia.
Ponieważ wysokość kopca zupełnego jest logarytmiczna ze względu na ilość węzłów, operacja wstawiania elementu do kopca odbywa się w czasie logarytmicznym.
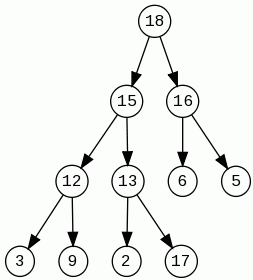


Usuwanie największego elementu – delete max
Usuwamy korzeń. W miejsce korzenia wkładamy prawy skrajny liść. Wymieniamy go miejscami z większym z potomków, następnie z większym z potomków węzła w nowej pozycji. Operację wykonujemy tak długo aż obaj potomkowie będą mniejsi lub element stanie się liściem.
Ponieważ wysokość kopca zupełnego jest logarytmiczna ze względu na ilość węzłów, operacja usuwania największego elementu odbywa się również w czasie logarytmicznym.

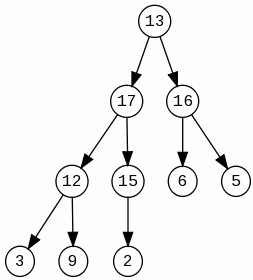
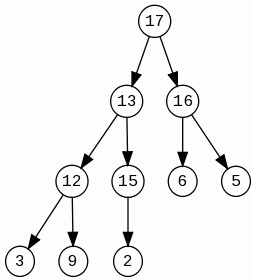

Operacja tworzenia kopca – construct:
Wykonując ją za pomocą wielokrotnego wstawiania elementów, mielibyśmy czas O(nlog n). Daje się jednak wykonać kopiec w czasie liniowym działając rekurencyjnie na podkopcach.
Wrzucamy elementy nieuporządkowane. Procedura construct wywołuje siebie rekurencyjnie dla prawego i lewego potomka. Wówczas mamy już dwa uporządkowane podkopce. Ich rodzic niekoniecznie jest największy, więc wykonujemy tę samą procedurę przemieszczania go w stronę liścia jak przy delete max.
Testy pokazały że naiwna konstrukcja za pomocą wielokrotnego insert jest niewiele wolniejsza w przypadku wstawiania losowych liczb; znacząca różnica staje się przy niekorzystnym przypadku wstawiania kolejnych coraz większych liczb.
- w korzeniu kopca znajduje się największy lub jeden z grupy największych o identycznej wartości,
- na ścieżkach (połączeniach między węzłami), od korzenia do liścia, elementy są posortowane nierosnąco

|
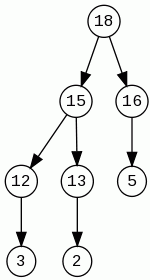
|
| kopiec zupełny | kopiec niezupełny |
Kopiec zupełny – to kopiec będący zupełnym drzewem binarnym. Drzewo binarne jest zupełne wtedy gdy wszystkie poziomy z wyjątkiem ostatniego są całkowicie zapełnione a na ostatnim liście są spójnie ułożone od strony lewej do prawej.
Na poziomie i z wyjątkiem ostatniego jest 2i węzłów
Wysokość takiego kopca jest logarytmiczna względem jego wielkości.
Kopiec zupełny można wygodnie reprezentować w tablicy o indeksie rozpoczynającym się od 1. Następniki węzła k mają numery 2k oraz 2k+1 a poprzednik węzła k ma wartość k/2 (dzielenie bez reszty - np. dla 7 rodzic ma numer 7/2 = 3).
Szczególne własności kopców zostały wykorzystane do stworzenia algorytmy do sortowania zwanego HeapSort
Kopiec pozwala również w wydajny sposób zaimplementować kolejkę priorytetową, gdzie dokładamy do niej różne elementy a wyjmujemy zawsze element największy.
Operacja wstawiania – insert
Operacja usuwania - delete max
Operacja wstawiania elementu do stosu insert:
Wstawiamy element w pierwsze wolne miejsce ostatniego poziomu, a następnie jeżeli wstawiony element jest większy od rodzica, zamieniamy go miejscami. Następnie po zamianie znów sprawdzamy, czy element jest większy od nowego rodzica. Jeżeli tak to znów zamieniamy do miejscami. Operację sprawdzania i zamieniania miejscami powtarzamy tak długo, aż w końcu rodzic będzie większy od wstawionego elementu bądź dojdziemy do korzenia.
Ponieważ wysokość kopca zupełnego jest logarytmiczna ze względu na ilość węzłów, operacja wstawiania elementu do kopca odbywa się w czasie logarytmicznym.



Usuwanie największego elementu – delete max
Usuwamy korzeń. W miejsce korzenia wkładamy prawy skrajny liść. Wymieniamy go miejscami z większym z potomków, następnie z większym z potomków węzła w nowej pozycji. Operację wykonujemy tak długo aż obaj potomkowie będą mniejsi lub element stanie się liściem.
Ponieważ wysokość kopca zupełnego jest logarytmiczna ze względu na ilość węzłów, operacja usuwania największego elementu odbywa się również w czasie logarytmicznym.




Operacja tworzenia kopca – construct:
Wykonując ją za pomocą wielokrotnego wstawiania elementów, mielibyśmy czas O(nlog n). Daje się jednak wykonać kopiec w czasie liniowym działając rekurencyjnie na podkopcach.
Wrzucamy elementy nieuporządkowane. Procedura construct wywołuje siebie rekurencyjnie dla prawego i lewego potomka. Wówczas mamy już dwa uporządkowane podkopce. Ich rodzic niekoniecznie jest największy, więc wykonujemy tę samą procedurę przemieszczania go w stronę liścia jak przy delete max.
Testy pokazały że naiwna konstrukcja za pomocą wielokrotnego insert jest niewiele wolniejsza w przypadku wstawiania losowych liczb; znacząca różnica staje się przy niekorzystnym przypadku wstawiania kolejnych coraz większych liczb.
Implementacje
| Autor | Język programowania | Komentarz | Otwórz | Pobierz | Ocena |
| Andrzej Borucki | C# | .cs | .cs | ***** / 5 | |
| Marek Rusinowski | C/C++ | Jest to klasa kopca. Oceniać :) W pliku kopiec.h znajduje się opis funkcji publicznych klasy. | .cpp | .cpp | ***** / 12 |
| Emil Hotkowski | C/C++ | Kopiec C++ | .cpp | .cpp | ***** / 14 |
| Mateusz Lewko | C/C++ | Prosto napisany kopiec. Polecam :) | .cpp | .cpp | ***** / 18 |
| Marek Rynarzewski | Php | .php | .php | ***** / 2 |
Poprawiony: 27 sierpnia 2015 07:05



Tomasz tylko uświadamiał Piotr'a że się myli ;)
zamieniając elementy tak aby otrzymać kopiec zaczynamy od liści czy od korzenia??
czy to nie ma znaczenia??
chodzi mi o formalną definicję i praktyczne zastosowanie...